A farmer has 240 meters of fencing material to enclose his rectangular plot of land. However, it is bound on one side by a river, and on the opposite side, half the fencing is purchased and supplied by the farmer that owns the lot. See below?
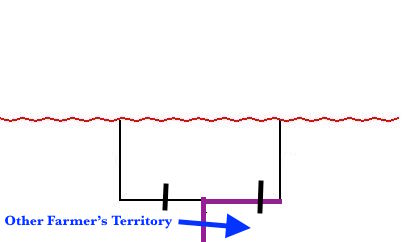
What is the maximum area of the farmer can make with this amount of fencing material and what will be the dimensions?

What is the maximum area of the farmer can make with this amount of fencing material and what will be the dimensions?
1 Answer
Sep 24, 2016
Let
The perimeter is given by:
The area is given by:
A = xy
The maximum area will be the vertex:
The vertex is at
Hence, the maximum area is given by dimensions of
Hopefully this helps!

