A gas at a constant volume has an initial temperature of 300.0 K and an initial pressure of 10.0 atm. What pressure does the gas exert at a temperature of 500.0 K?
1 Answer
Explanation:
As you know, gas pressure is caused by the collisions between the gas molecules and the walls of the container.
The more powerful and frequent these collisions are, the higher the pressure exerted by the gas.
Now, temperature is actually a measure of the average kinetic speed of the gas molecules. This means that increasing the temperature of a gas is equivalent to increasing the average kinetic energy of its molecules.
When volume and number of moles of gas are kept constant, increasing the temperature of the gas will result in an increase in pressure - this is known as Gay Lussac's Law.
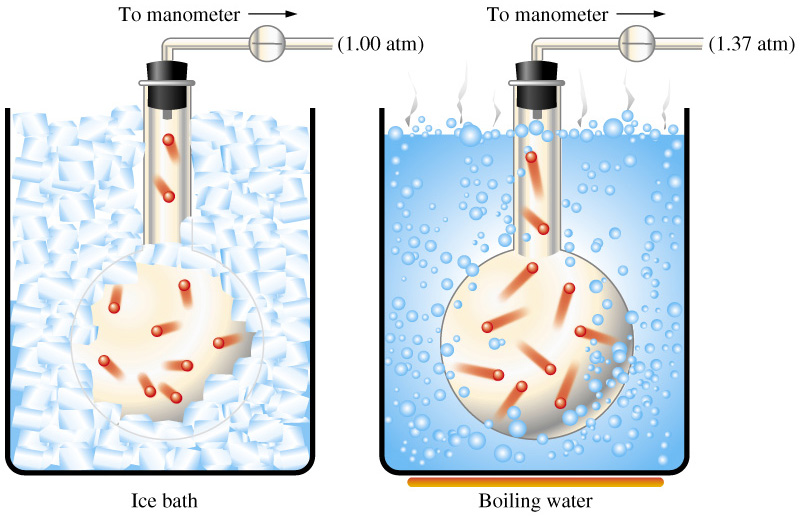
This happens because if the molecules are moving at a higher average kinetic energy, they will hit the walls of the container with more force and more frequent
Mathematically, this is written as
#color(blue)(|bar(ul( color(white)(a/a)P_1/T_1 = P_2/T_2color(white)(a/a)|)))" "# , where
It's very important to remember that the temperature of the gas must be expressed in Kelvin!
So, rearrange the equation to solve for
#P_2 = T_2/T_1 * P_1#
Plug in your values to find
#P_2 = (500.0 color(red)(cancel(color(black)("K"))))/(300.0color(red)(cancel(color(black)("K")))) * "10.0 atm" = "16.667 atm"#
Rounded to three sig figs, the number of sig figs you have for the initial pressure of the gas, the answer will be
#P_2 = color(green)(|bar(ul(color(white)(a/a)"16.7 atm"color(white)(a/a)|)))#

