Question

A rectangle is inscribed in an equilateral triangle so that one side of the rectangle lies on the base of the triangle. How do I find the maximum area of the rectangle when the triangle has side length of 10?

Answer 1

`A = (25sqrt(3))/2`

Explanation:

First, let's look at a picture.

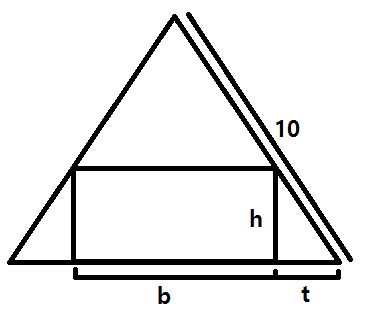
Some initial observations:

• The area `A` of the rectangle is `A=bh`.

• By symmetry, the base of the triangle is of length `b+2t`, and thus, as it is of length `10`, we have `b+2t = 10 => t = 5-b/2`

• If we decide `b` that also determines `h`, and thus we can write `h` as a function of `b`.

To write `h` as a function of `b`, we can look at the right triangle with legs `t` and `h`. As it shares an angle with an equilateral triangle, we know it is a `30^@`-`60^@`-`90^@` triangle, and thus `t/h = 1/sqrt(3)`.
Solving for `h` gives us `h = sqrt(3)t = sqrt(3)(5-b/2)` by our initial observation.

Then, we can rewrite our formula for the area as

`A = b*sqrt3(5-b/2) = sqrt(3)(-1/2b^2 + 5b)`

If we look at the graph for `A` we will see it is a downward facing parabola, and thus will have a maximum at its vertex. Then, we can complete the square to find

`A = sqrt(3)(-1/2b^2+5b)`
`= -sqrt(3)/2(b^2-10b)`
`= -sqrt(3)/2((b-5)^2-25)`

And so the vertex, and thus the maximum area, is at `b = 5`.

Finally, we calculate the area from this to get

`A = -sqrt(3)/2((5-5)^2-25) = (25sqrt(3))/2`