A rectangle is inscribed with its base on the x axis and its upper corners on the parabola y = 12 − x^2. What are the dimensions of such a rectangle with the greatest possible area?
1 Answer
The greatest area occurs when the rectangle has a width of 4 and a height of 8 leading to a maximum area of 32
Explanation:
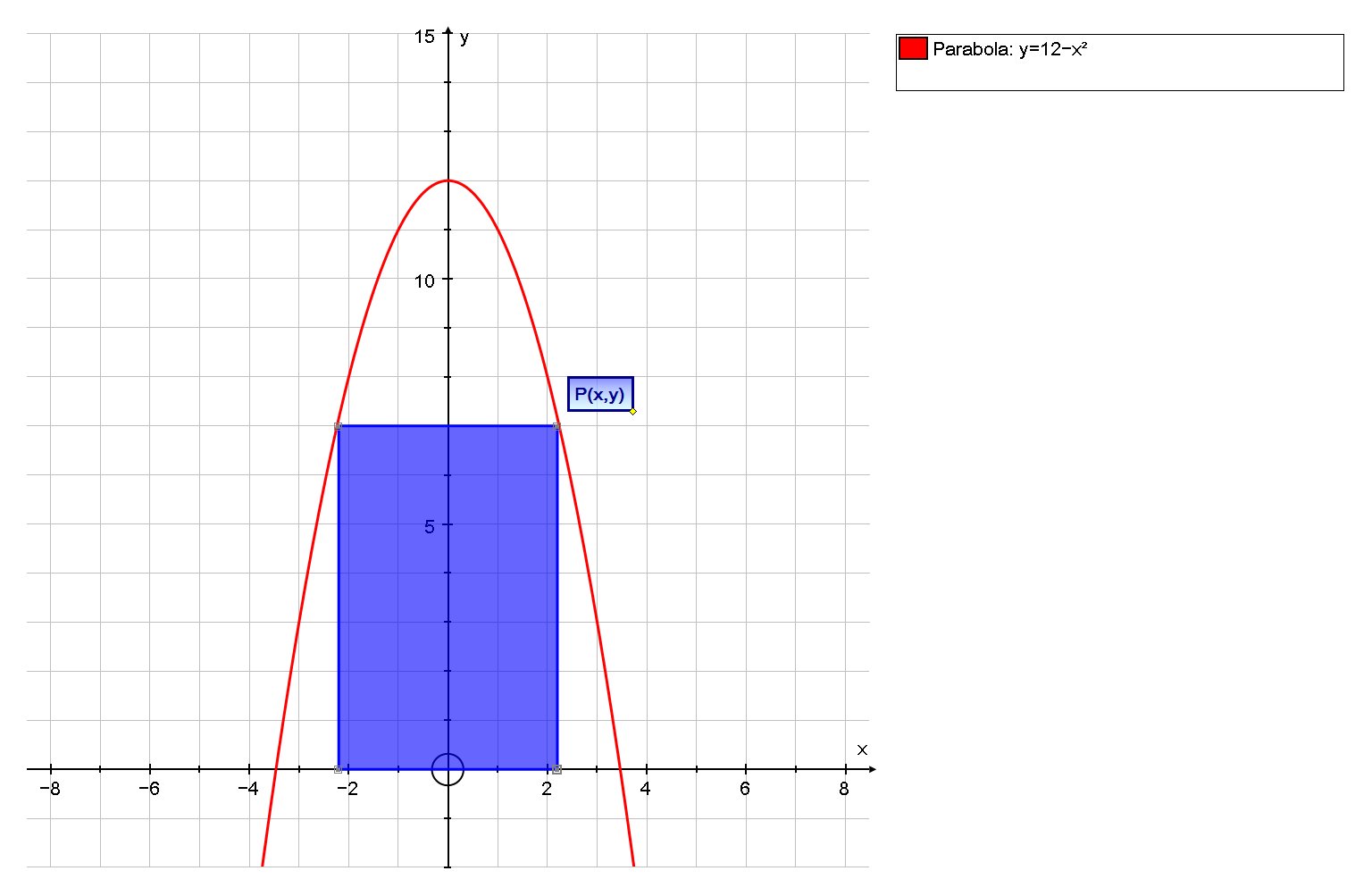
Let us set up the following variables:
# {(P(x,y), "coordinate of the right hand corner"), (A, "Area of Rectangle") :} #
Due to symmetry The width of the rectangle is half the distance between P and the y-axis, ie
Width =
#2x# and Height=#y#
Hence the Area of the rectangle is:
# \ \ \ \ \ A = Wdith xx Height #
# :. A = 2xy #
# :. A = 2x(12-x^2) #
# :. A = 24x-2x^3) # ..... [1]
We are asked to maximise the Area as
Differentiating [1] wrt
At a critical point,
# :. 24-6x^2 = 0#
# :. 6x^2 = 24#
# :. x^2 = 4#
# :. x = +-2#
Obviously
# :. x = 2#
We need to check if this is a max or a min, so differentiate [2] wrt
# :. (d^2A)/dx^2 = -12x #
# :. (d^2A)/dx^2 = -12x < 0 " when " x=2# , confirming a max
When
Width =
#2*2 = 4#
Height =#12-4=8#
Area =#32#

