A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is #12 # and the height of the cylinder is #18 #. If the volume of the solid is #72 pi#, what is the area of the base of the cylinder?
1 Answer
Sep 7, 2016
The area of the base is
Explanation:
Start by drawing a diagram.
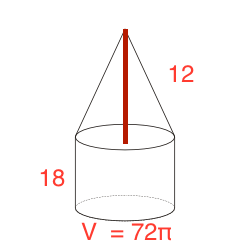
The formula for volume of a cone is
Let
The formula for area of a circle is
Hopefully this helps!

