Question

A triangle has corners A, B, and C located at `(4 ,3 )`, `(7 ,4 )`, and `(2 ,8 )`, respectively. What are the endpoints and length of the altitude going through corner C?

Answer 1

See below.

Explanation:

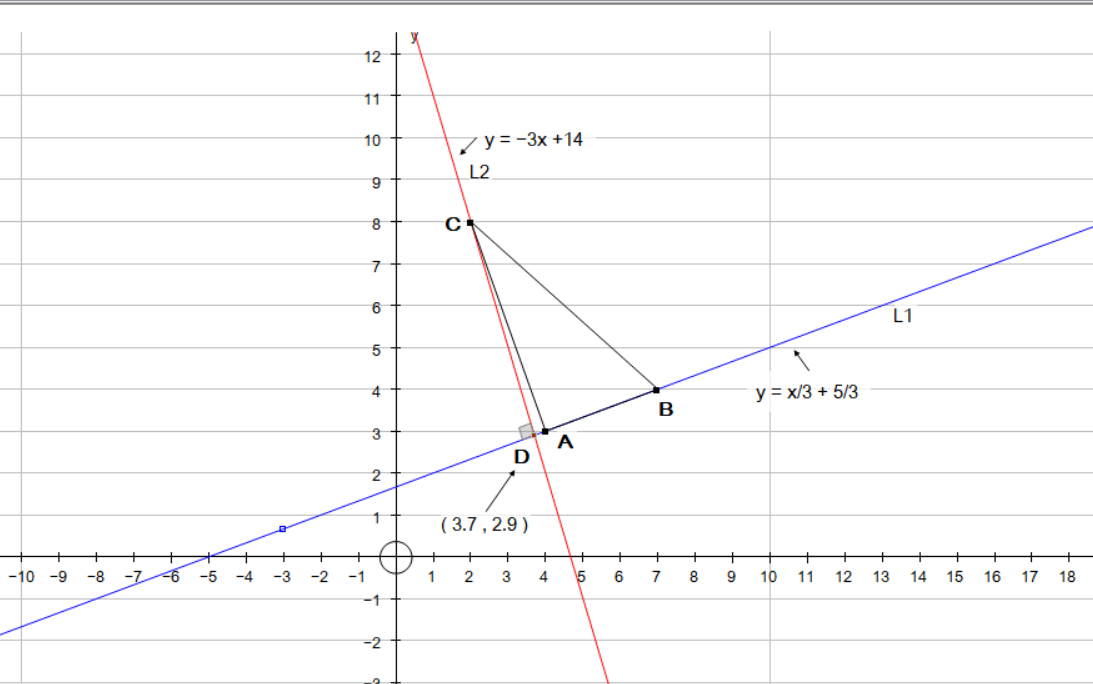
If a line passes through points A and B, we will call this `l_1` and another line `l_2` passes through point C and meets `l_1` at right angles, then this point of intersection will be one of the end points of altitude going through C. See diagram.

First we have to find the equation of the line `l_1`. We can do this by using the coordinates of A and B.

First find the gradient:

`(4-3)/(7-4)=1/3`

`:.`

`y-3=1/3(x-4)=>y=1/3x+5/3color(white)(888)[ l_1]`

For `l_2`. We know that if two lines are perpendicular, then the product of their gradients is `-1`. So:

`1/3*m_2=-1=>m_2=-3`

Using the coordinates of point C:

`l_2=y-8=-3(x-2)=>l_2=y=-3x+14color(white)(888)[l_2]`

For the point of intersection of `[l_1] and [l_2]`

Solving `l_1 and l_2` simultaneously.

`1/3x+5/3=-3x+14=>x=37/10`

`y = -3(37/10)+14=>y=29/10`

Coordinates of intersection:

`( 37/10 , 29/10 )`

So end points of altitude:

`color(blue)((( 37/10 , 29/10 )))` and point `C=color(blue)((( 2 , 8 )))`

Length of altitude:

`DC=sqrt((37/10-2)^2+(29/10-8)^2)=color(blue)(17/10sqrt(10)~~5.376)`

( 3 .d.p.)