Question

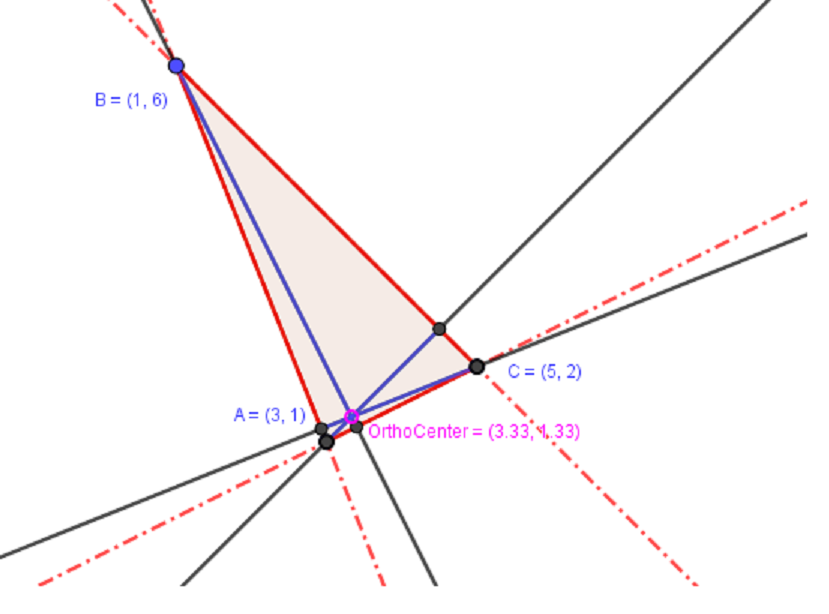
What is the orthocenter of a triangle with corners at `(3 ,1 )`, `(1 ,6 )`, and (5 ,2 )#?

Answer 1

Triangle with vertices at `(3 ,1 )`, `(1 ,6 )`, and `(5 ,2 )`.

Orthocenter = `color(blue)((3.33, 1.33)`

Explanation:

Given:

Vertices at `(3 ,1 )`, `(1 ,6 )`, and `(5 ,2 )`.

We have three vertices: `color(blue)(A(3,1), B(1,6) and C(5,2)`.

`color(green)(ul (Step:1`

We will find the slope using the vertices `A(3,1), and B(1,6)`.

Let `(x_1, y_1) = (3,1) and (x_2, y_2) = (1,6)`

Formula to find the slope (m) = `color(red)((y_2-y_1)/(x_2-x_1)`

`m=(6-1)/(1-3)`

`m=-5/2`

We need a perpendicular line from the vertex `C` to intersect with the side `AB` at `90^@` angle. To do that, we must find the perpendicular slope, which is the opposite reciprocal of our slope `(m)=-5/2`.

Perpendicular slope is `=-(-2/5) = 2/5`

`color(green)(ul (Step:2`

Use the Point-Slope Formula to find the equation.

Point-slope formula: `color(blue)(y=m(x-h)+k`, where
`m` is the perpendicular slope and `(h,k)` represent the vertex `C` at `(5, 2)`

Hence, `y=(2/5)(x-5)+2`

`y=2/5x-10/5+2`

`y=2/5x` `" "color(red)(Equation.1`

`color(green)(ul (Step:3`

We will repeat the process from `color(green)(ul (Step:1` and `color(green)(ul (Step:2`

Consider side `AC`. Vertices are `A(3,1) and C(5,2)`

Next, we find the slope.

`m=(2-1)/(5-3)`

`m=1/2`

Find the perpendicular slope.

`=rArr -(2/1) =- 2`

`color(green)(ul (Step:4`

Point-slope formula: `color(blue)(y=m(x-h)+k`, using the vertex `B` at `(1, 6)`

Hence, `y=(-2)(x-1)+6`

`y= -2x+8` `" "color(red)(Equation.2`

`color(green)(ul (Step:5`

Find the solution to the system of linear equations to find the vertices of the Orthocenter of the triangle.

`y=2/5x` `" "color(red)(Equation.1`

`y= -2x+8` `" "color(red)(Equation.2`

The solution is becoming too long. Method of Substitution will provide solution for the system of linear equations.

Orthocenter `=(10/3, 4/3)`

The construction of the triangle with the Orthocenter is: