What is the orthocenter of a triangle with corners at #(3 ,1 )#, #(4 ,5 )#, and (2 ,2 )#?
1 Answer
Orthocenter of the triangle ABC is
Explanation:
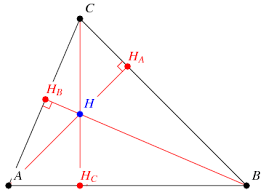
The steps to find the orthocenter are:
1. Find the equations of 2 segments of the triangle (for our example we will find the equations for AB, and BC)
-
Once you have the equations from step #1, you can find the slope of the corresponding perpendicular lines.
-
You will use the slopes you have found from step #2, and the corresponding opposite vertex to find the equations of the 2 lines.
-
Once you have the equation of the 2 lines from step #3, you can solve the corresponding x and y, which is the coordinates of the orthocenter.
Given (A(3,1), B(4,5), C(2,2)
Slope of AB
Slope of
Similarly, slope of BC
Slope of
Equation of
Equation of
Solving equations (1), (2), we get the coordinates of Orthocenter H.
