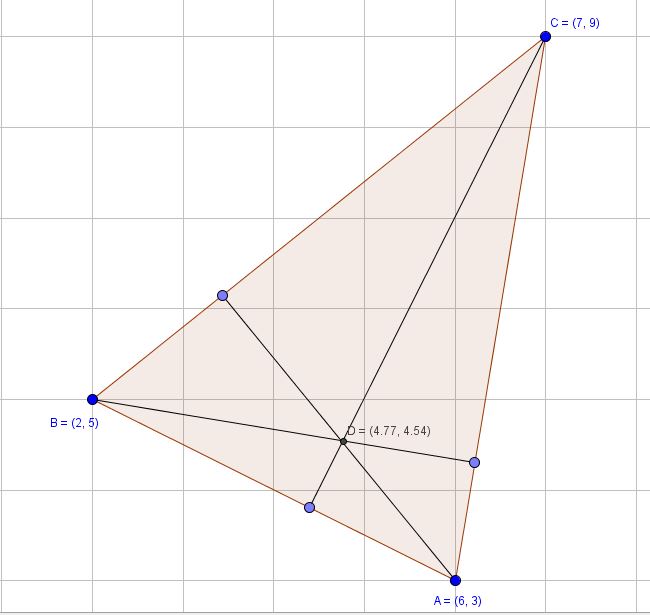
First find the equation of line of the side of the triangle,
#bar(AB), bar(BC) " and " bar(CA)#
Equation of line sets for: #color(red)(bar(AB))#:
#y_(bar(AB)) = m_(bar(AB)) x+b_(bar(AB))# with #m=(3-5)/(6-2)=-1/2#
Use B(2,5) which is on #y_(bar(AB)) = m_(bar(AB)) x+b_(bar(AB))#
Letting #y=5# and #x=2# solve for #b_(bar(AB))#
#5=-1/2*2+b_(bar(AB)); b_(bar(AB)) = 6# thus
#y_(bar(AB)) = -1/2 x+6#
A perpendicular equation of line will have a slope
#m_(bar(AB))=-1/m_(bar(AB)); -1/2=-1/m_(bar(AB));m_(Pr_bar(AB))= 2#
Thus the perpendicular equation of linr to AB is:
#y_(Pr_bar(AB)) = 2x+ b_(Pr_bar(AB))#
use #A(7,9)# to determine #b_(Pr_bar(AB))#
#9 = 2*7+ b_(Pr_bar(AB)); b_(Pr_bar(AB))=-5#
So the pair of equation sets, for #color(red)bar(AB)# are:
#[(y), (color(blue)(y_(pr)))]_(bar(AB)) = [(-1/2, 6) , (color(blue)(2), color(blue)(-5) )]*[(x), (1) ]#
Equation of line sets for: #color(red)(bar(BC))#:
#y_(bar(A=BC))=m_(bar(BC)) x+b_(bar(BC))# with #m=(9-5)/(7-2)=4/5#
#5=4/5*2+b; b=17/5# the perpendicular has slope and y-intercept:
#m_(pr) = -1/m; m_(pr)=-5/4#
Using point# A(6,3)# to determine #b_(pr)#:
#3=-5/4*6+b_(pr); b_(pr)=21/2#
#[(y), (color(magenta)(y_(pr)))]_(bar(BC)) = [(4/5, 17/5) , (color(magenta)(-5/4), color(magenta)(21/2))]*[(x), (1) ]#
The Orthocenter is the point where the perpendicular line to AB and BC meet, i.e.: #color(blue)(y_(Pr_bar(AB))) = color(magenta)(y_(Pr_bar(BC))#
#color(blue)(2x-5)=color(magenta)(-5/4x +21/2); x=62/13#
Using x=62/13 solve for y:
#y=2x-5|_(x=(62/13))#, #y=2*62/13-5= 59/13#