Question

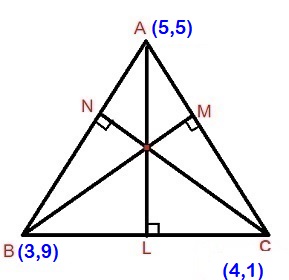
A triangle has corners A, B, and C located at `(5 ,5 )`, `(3 ,9 )`, and `(4 , 1 )`, respectively. What are the endpoints and length of the altitude going through corner C?

Answer 1

The end points of altitude `CD` is `(4,1) and (6.4,2.2)`
Length of altitude `CD ~~ 2.68` unit

Explanation:

`A(5,5) , B(3,9) , C(4,1)`

Let `CD` be the altitude going through `C` touches `D` on line

`AB`. `C` and `D` are the endpoints of altitude `CD; CD` is

perpendicular on `AB`. Slope of `AB= m_1= (y_2-y_1)/(x_2-x_1)`

`=(9-5)/(3-5) = 4/(-2) =-2 :.` Slope of

`CD=m_2= -1/m_1= 1/2`

Equation of line `AB` is `y - y_1 = m_1(x-x_1)`or

`y- 5 = -2(x-5) or 2 x+y = 15 ; (1)`

Equation of line `CD` is `y - y_3 = m_2(x-x_3)` or

`y- 1 = 1/2(x-4) or 2 y-2= x-4 or 2 y - x =-2 ;(2)`

Sollving equation (1) and (2) we get

the co-ordinates of `D(x_4,y_4)`. Mutiplying equation (2) by `2`

we get `-2x+4y=-4 ; (3)` , adding equation (1) from

equation (3) we get `5 y=11 or y=11/5=2.2`

`:. x=(15-y)/2=(15-2.2)/2=6.4 :. D` is `(6.4,2.2,)`.

The end points of altitude `CD` is `(4,1) and (6.4,2.2)`

Length of altitude `CD` is

`CD = sqrt((x_3-x_4)^2+(y_3-y_4)^2)` or

`CD = sqrt((4-6.4)^2+(1-2.2)^2)= sqrt 7.2 ~~ 2.68` unit [Ans]

Answer 2

The endpoints of altitude are :C(4,1) and N(32/5,11/5).
The length of altitude is :`CN=sqrt(36/5)`

Explanation:

Let `triangleABC " be the triangle with corners at"`

`A(5,5), B(3,9) and C(4,1)`

Let `bar(AL) , bar(BM) and bar(CN)` be the altitudes of sides `bar(BC) ,bar(AC) and bar(AB)` respectively.

Let `(x,y)` be the intersection of three altitudes

Slope of `bar(AB) =(5-9)/(5-3)=-4/2=-2`

`bar(AB)_|_bar(CN)=>`slope of `bar(CN)=1/2` ,

`bar(CN)` passes through `C(4,1)`

`:.`The equn. of `bar(CN)` is `:y-1=1/2(x-4)`

`=>2y-2=x-4`

`=>x-2y=2`

`i.e. color(red)(x=2y+2.....to (1)`

Now, Slope of `bar(AB) =-2` and `bar(AB)` passes through
`A(5,5)`

So, eqn. of `bar(AB)` is: `y-5=-2(x-5)`

`=>y-5=-2x+10`

`=>color(red)(y=15-2x...to(2)`

From `(1)and (2)`

`y=15-2(2y+2)=15-4y-4=11-4y`

`=>y+4y=11=>5y=11=>color(blue)(y=11/5`

From `(1) ,`

`x=2(11/5)+2=>color(blue)(x=32/5`

`=>N(32/5,11/5) and C(4,1)`

Using Distance formula,

`CN=sqrt((32/5-4)^2+(11/5-1)^2)=sqrt(144/25+36/25)`
`:.CN=sqrt(180/25)`

`:.CN=sqrt(36/5)~~2.68`