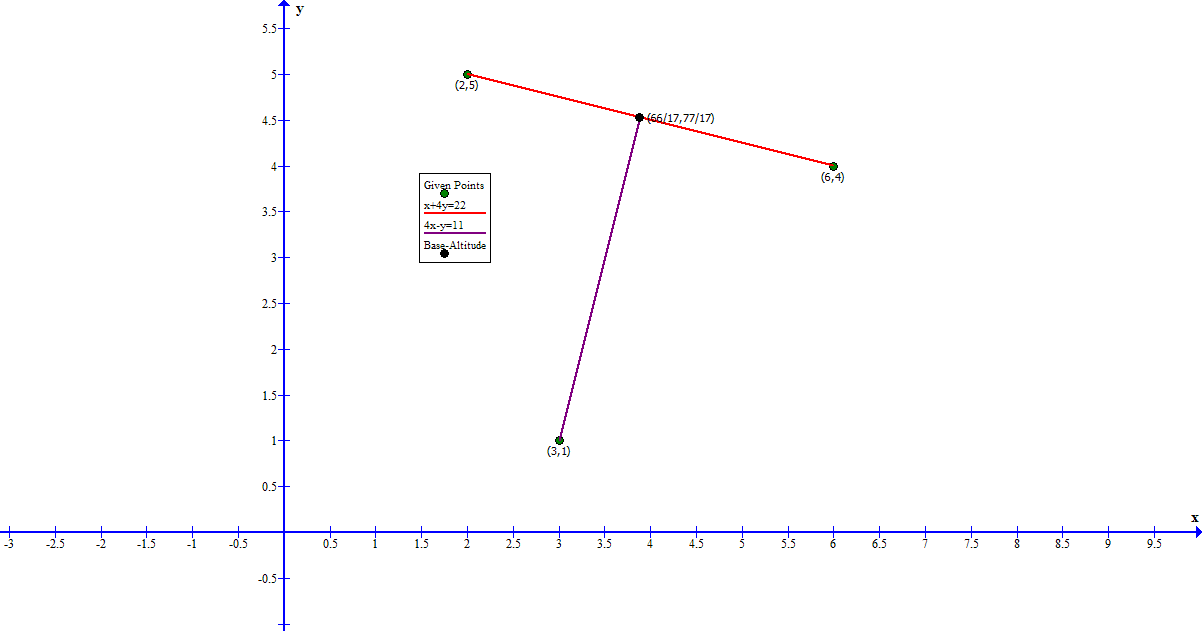
The line segment #AB# with #A=(6,4)# and #B=(2,5)#
has a slope of #m_(AB)=(5-4)/(2-6)=-1/4#
Using the point #A# and this altitude we can develop an equation for this line using the slope-point form:
#color(white)("XXX")y-4=(-1/4)(x-6)#
#color(white)("XXX")4y-16=6-x#
#color(white)("XXX")x+4y= 22#
#color(teal)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")#
The altitude through #C=(3,1)# is perpendicular to the base #AB#
and therefore the altitude has a slope of #m_("alt")=-1/(m_(AB))=4#
Using the point #C# and the slope of the altitude we can develop an equation for the altitude using the slope-point form:
#color(white)("XXX")y-1=4(x-3)#
#color(white)("XXX")y-1=4x-12#
#color(white)("XXX")4x-y=11#
#color(teal)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")#
The point where the altitude intersects the base can be found as the solution to the set of equations:
[1]#color(white)("XXX")x+4y=22#
[2]#color(white)("XXX")4x-y=11#
Adding [1] and #4# times [2]
#color(white)("XXXXXX")x+4y=22#
#color(white)("XXXXX")underline(16x-4y=44)#
[3]#color(white)("XXXX")17xcolor(white)("XXX")=66#
or (after dividing by #17#)
[4]#color(white)("XXX")x=66/17#
Similarly, multiplying [1] by #4# and subtracting [2]
#color(white)("XXXXXX")(4x+16y)=color(white)("Xx")(88)#
#color(white)("XXXxX")underline(-(4x-color(white)("Xx")y)=-(11))#
[5]#color(white)("XXXXXXXxX")17y=color(white)("XxX")77#
or (after dividing by #17#)
[6]#color(white)("XXX")y=77/17#
#color(teal)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")#
To find the length of the altitude use the Pythagorean Theorem
to calculate the distance from #(3,1)# to #(66/17,77/17)#
#color(white)("XXX")"Alt." = sqrt((3-66/17)^2+(1-77/17)^2)#
Using a calculator, this approximates as
#color(white)("XXX")"Alt."~~3.638#

