#color(red)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")#
Overview of Solution Method
1. Find slope of AB
2. Find equation of line through A and B
3. Find equation of line through C perpendicular to AB
4. Find coordinates of intersection of the two equations.
5. Find length of line segment between C and point of intersection.
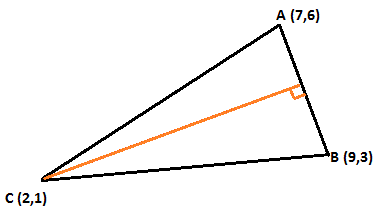
#color(red)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")#
#underline(color(blue)("1. Find slope of AB"))#
#color(white)("XXX")"slope"_(AB) = (y_B-y_A)/(x_B-x_A)#
#color(white)("XXXXXXXX")=(3-6)/(9-7)#
#color(white)("XXXXXXXX")=-3/2#
#underline(color(blue)("2. Find equation of line through A and B"))#
Using the #"slope"_(AB)# from 1. and point A coordinates with the point-slope form:
#color(white)("XXX")(y-6)=-3/2(x-7)#
or
#color(white)("XXX")3x+2y=33#
#underline(color(blue)("3. Find equation of line through C perpendicular to AB"))#
Recalling that the slopes of perpendicular lines are the negative inverse of each other,
the slope of any line perpendicular to AB must be #2/3#.
Using this slope and the coordinates for point C with the point-slope form:
#color(white)("XXX")(y-1)=2/3(x-2)#
or
#color(white)("XXX")2x-3y=1#
#underline(color(blue)("4. Find coordinates of intersection of the two equations"))#
#color(white)("XXX"){(3x+2y=33color(white)("XXXX")[1]),(2x-3y=1color(white)("XXXxX")[2]):}#
#color(white)("XXX")
{
(6x+4y=66color(white)("XXXX")[1]xx2),
(6x-9y=3color(white)("XXXxX")[2]xx3)
:}#
#color(white)("XXX")rarr13y=63color(white)("XX") rarrcolor(white)("XX") y=63/13#
#color(white)("XXX")
{
(9x+6y=99color(white)("XXXX")[1]xx3),
(4x-6y=2color(white)("XXXxX")[2]xx2)
:}#
#color(white)("XXX")rarr 13x=101color(white)("XX")rarrcolor(white)("XX")x=101/3#
#color(white)("XXX")"Base of altitude on AB is at "(x,y)=(101/13,63/13)#
#underline(color(blue)("5. Find length of line segment between C and point of intersection"))#
Using the Pythagorean Theorem:
#color(white)("XXX")#Length of altitude to AB from C
#color(white)("XXX")=sqrt((2-101/13)^2+(1-63/13)^2)#
#color(white)("XXX")~~6.933752# (using a calculator)

