Given:
#color(white)("XXX")A=(8,3)#
#color(white)("XXX")B=(4,5)#
#color(white)("XXX")C=(6,7)#
First let's consider the line through #A# and #B#
#color(white)("XXX")"slope"_(AB)=(5-3)/(4-8)=-1/2#
#color(white)("XXX")#using the point-slope form the equation of the line through #A# and #B# is
#color(white)("XXXXXX")(y-3)=-1/2(x-8)#
#color(white)("XXXXXX")2y-6 =8-x#
#color(white)("XXXXXX")x+2y=14#
Looking at the altitude from #AB# through #C#
#color(white)("XXX")#The altitude line is always perpendicular to the base.
#color(white)("XXX")#Therefore
#color(white)("XXX")"slope"_"Alt"= 2# ...since the base has a slope of #(-1/2)#
#color(white)("XXX")#using the slope-point form the equation of the altitude line through #C# is
#color(white)("XXXXXX")y-7=2(x-6)#
#color(white)("XXXXXX")y-7=2x-12#
#color(white)("XXXXXX")2x-y=5#
Finding the point of intersection of the altitude with the base #AB#
#color(white)("XXX")#We have
#color(white)("XXXXXX"){(x+2y=14),(2x-y=5):}#
#color(white)("XXX")#Using standard solution techniques:
#color(white)("XXXXXX")(x,y)=(24/5,23/5)#
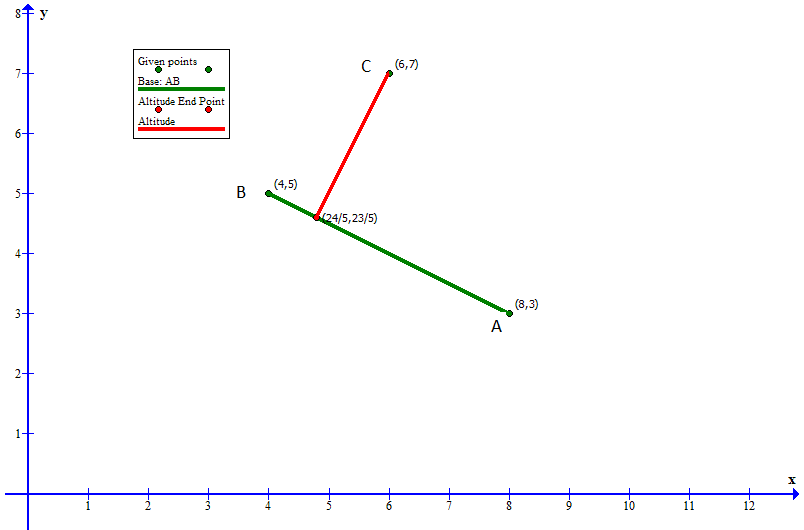
Calculating the length of the Altitude
#color(white)("XXX")#Using the Pythagorean Theorem
#color(white)("XXX")#with endpoints #(6,7)# and #(24/5,23/5)#
#color(white)("XXXXXX")abs("alt")=sqrt((6-24/5)^2+(7-23/5)^2)#
#color(white)("XXXXXXXX")~~2.68# (using calculator/spreadsheet)

