A triangle has corners A, B, and C located at #(8 ,7 )#, #(4 ,5 )#, and #(6 , 7 )#, respectively. What are the endpoints and length of the altitude going through corner C?
1 Answer
Explanation:
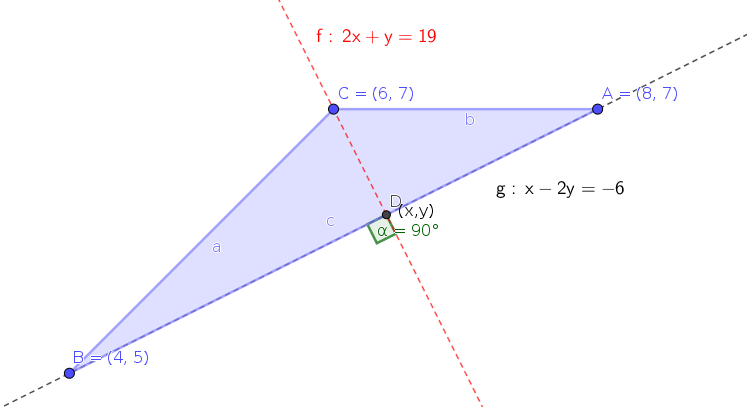
-
Let's find the equation of the g line that passes through the triangle A and the B corner.
-
If the coordinates of two points of a line are known, then the equation of that line is written as follows.
-
# (y_2-y_1)/(x_2-x_1)=(y-y_2)/(x-x_2) # -
#A(8,7) , B(4,5) , x_1=8 , y_1=7 , x_2=4 , y_2=5# -
# (5-7)/(4-8)=(y-5)/(x-4)# -
#(-2)/(-4)=(y-5)/(x-4)# -
#1/2=(y-5)/(x-4)# -
#x-4=2y-10# -
#x-2y=-6 " (1) equation of line g"# -
#y=1/2 x+3 # -
If the equation is written in the form y = m x + n, m gives the slope. m=
#1/2# -
The altitude passing through the corner C will be perpendicular to line g.
-
Let D (x, y) be the intersection point.
-
multiplied by the slopes of two straight lines perpendicular to each other equal to -1.
-
#1/2 * m_f=-1 " , " m_f=-2# -
#y-y_1=m(x-x_1# -
#y-7=-2(x-6)" , "y-7=-2x+12# -
#y+2x=19 " " (2)" the f line"# -
Now we have two equations((1) and (2)).
-
(2) We multiply both sides of the equation by 2.
-
#2y+4x=38 " "(3)# -
#x-2y=-6" "(1) # -
Let's sum up the equations (1) and (3) we get .
-
5x=32 , x=6.4
-
In equation (1) or (3) we write 6.4 instead of x
-
6.4 -2y=-6 , -2y=-12.4 , y=6.2
-
The coordinates of D (x, y) are (6.4, 6.2).
-
length=
#sqrt((6.4-6)^2+(6.2-7)^2)# -
length=
#sqrt((0.4)^2+(-0.8)^2)# -
length=
#sqrt((0.16)+(0.64))# -
length=
#0.89#

