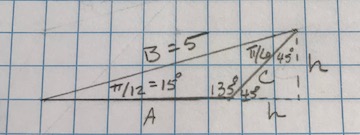Given: A triangle with angles #pi/12 (15^o), pi/6 (30^o), (3 pi)/4 (135^o)# and #B=5#
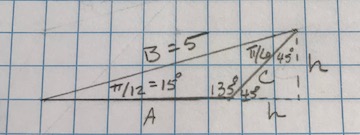
There are multiple ways to solve this problem. You can use the formula: #Area = 1/2 "Base" * "height"# or you can use Heron's formula which requires you to find the length of all sides.
Find the area using #Area = 1/2 "Base" * "height"#:
Find the height:
#" "sin (pi/12) = h/5 " so "h = 5 sin( pi/12)~~1.294#
Find the base A:
You can use the Pythagorean Theorem or trigonometry to find #A + h#:
#sin (30^o + 45^o) = sin(75^o) = (A+h)/5#
#A +h = 5 sin 75^o#
#A = 5 sin 75^o - h = 5 sin 75^o - 5 sin( pi/12) = 5(sin 75^o -sin(pi/12)) ~~ 3.536#
#Area = 1/2 * 3.536 * 1.294~~ 2.29 "units"^2#
Find the Area using Heron's Formula:
#s = (A + B + C)/2; Area = sqrt(s(s-A)(s-B)(s-C))#
Since we have a #45^o - 45^o - 90^o# triangle formed with the height, we have the ratio: #h: h: h sqrt(2)# for side lengths.
This means #C = h sqrt(2) = 5 sqrt(2) sin (pi/12) ~~1.83#
From above, #A = 5(sin 75^o -sin(pi/12))~~3.536#
#s ~~ 5.183#
#Area = sqrt(5.183(1.647)(.183)(3.353)) ~~2.29 "units"^2#