A triangle has sides A, B, and C. If the angle between sides A and B is #(pi)/8#, the angle between sides B and C is #(5pi)/12#, and the length of B is 1, what is the area of the triangle?
1 Answer
Feb 25, 2017
1.23
Explanation:
For sake of easy calculations, the angle measures in degrees would be
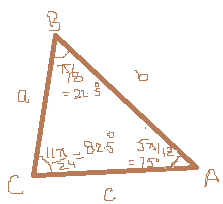
Now using
Thus
Now for using Heron formula for the area of a triangle,
(s-a)= 0.53, (s-b)= 2.05, and (s-c)= 0.46
Area of Triangle would be=
