A triangle has sides A, B, and C. If the angle between sides A and B is #(pi)/8#, the angle between sides B and C is #(pi)/3#, and the length of B is 2, what is the area of the triangle?
1 Answer
May 10, 2016
Area= 0.6685
Explanation:
The triangle ABC and its given components would be as shown in the figure. Angle B=
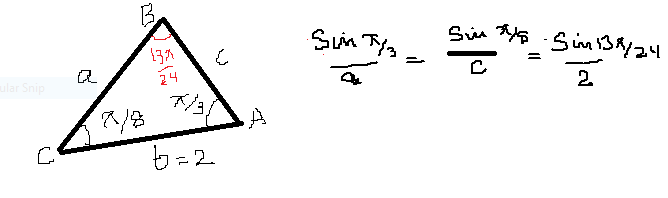
a =
To find the area length of perpendicular fro B upon side b is required . It would be a
Area=
= a
=0.6685
