A triangle has sides A, B, and C. Sides A and B are of lengths 4 and 5, respectively, and the angle between A and B is pi/4. What is the length of side C?
2 Answers
Explanation:
In this case, we can use the law of cosines. The law of cosines works when you have any triangle, and you know the value of two side lengths and one angle in between (which would be the case in this problem). Using the formula:
Where
Explanation:
According to the law of cosines,
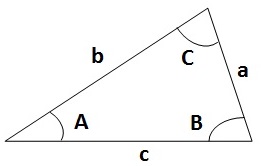
We know that


