A triangle has sides A, B, and C. Sides A and B have lengths of 3 and 6, respectively. The angle between A and C is #(pi)/8# and the angle between B and C is # (pi)/24#. What is the area of the triangle?
1 Answer
This triangle is not possible.
Explanation:
We begin by attempting to draw the triangle in question. Let's start with the vertex for the first angle that we were given. This is the angle between sides A and C which is
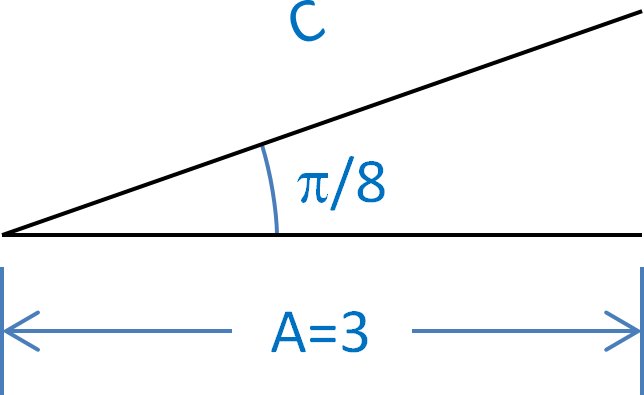
We know that side B has length 6 units - twice as long as side A. It becomes clear that to draw B, it must be at a large angle to A, which makes sense from the angle we got for the vertex between B and C which is a very small angle
Attempting to complete the triangle using a side of 6 units at the prescribed angles:
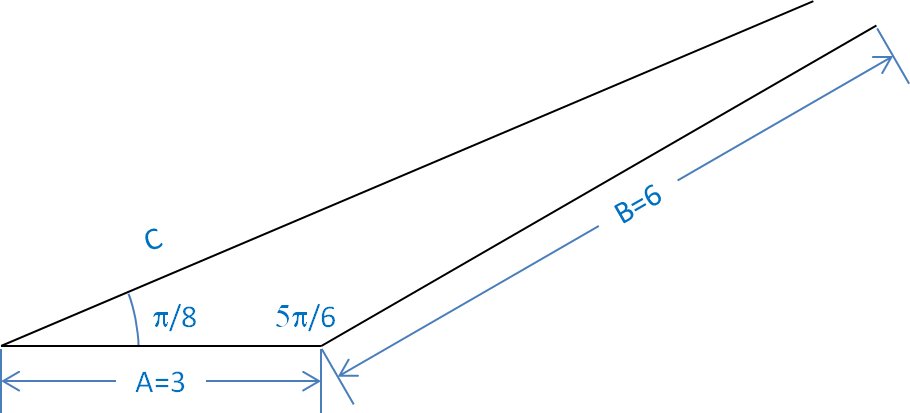
We come to realize that this is not a possible triangle - there is no way to make side B meet side C. Either one of the angles given is wrong or one of the lengths is wrong.

