A triangle has sides A, B, and C. Sides A and B have lengths of 6 and 20, respectively. The angle between A and C is #(17pi)/24# and the angle between B and C is # (pi)/8#. What is the area of the triangle?
1 Answer
Dec 16, 2015
22.96 (approx) sq units
Explanation:
Sides are marked with small letters. So the sides are a,b,c. Triangle is ABC. Side opposite A is a, side opposite B is b...... The triangle is like this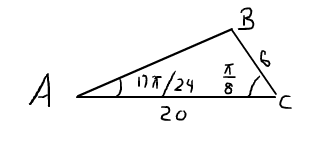
The area of the triangle would be
=
For exact value write
