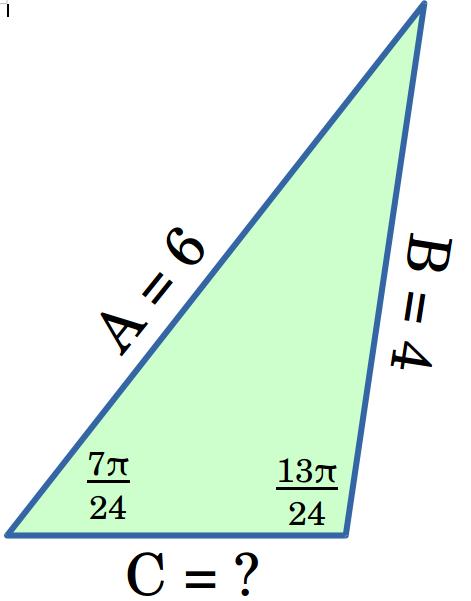
A triangle has sides A, B, and C. Sides A and B have lengths of 6 and 4, respectively. The angle between A and C is #(7pi)/24# and the angle between B and C is # (13pi)/24#. What is the area of the triangle?
1 Answer
Let us plot the triangle, and let us find its area using trigonometry.
Explanation:
First of all, our triangle is similar to the next one:
Although there are many ways to find the area of a triangle (you can check it on Wikipedia ), we will use trigonometry:
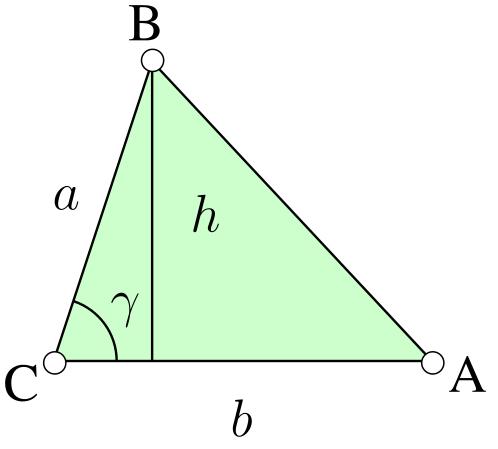
The area of the above triangle can be calculated by:
i.e. we must multiply two sides and the sine of the angle between them.
We know A and B sides, but we do not know the angle. We may calculate it by knowing that, for any triangle with angles
And now:

