A triangle has sides A, B, and C. The angle between sides A and B is #(2pi)/3# and the angle between sides B and C is #pi/12#. If side B has a length of 16, what is the area of the triangle?
1 Answer
Mar 5, 2016
Two angles of the triangle are
So the third angle between sides A and C
Pl consider the fig. below
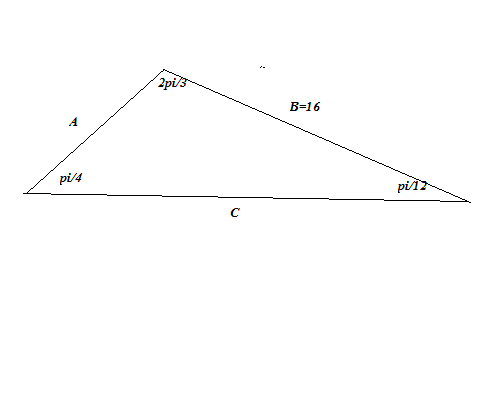
From Properties of triangle we know the sides of a triangle are proportional to the
Now area of the triangle

