A triangle has sides A, B, and C. The angle between sides A and B is #(3pi)/4#. If side C has a length of #16 # and the angle between sides B and C is #pi/12#, what are the lengths of sides A and B?
1 Answer
Side
:)
Explanation:
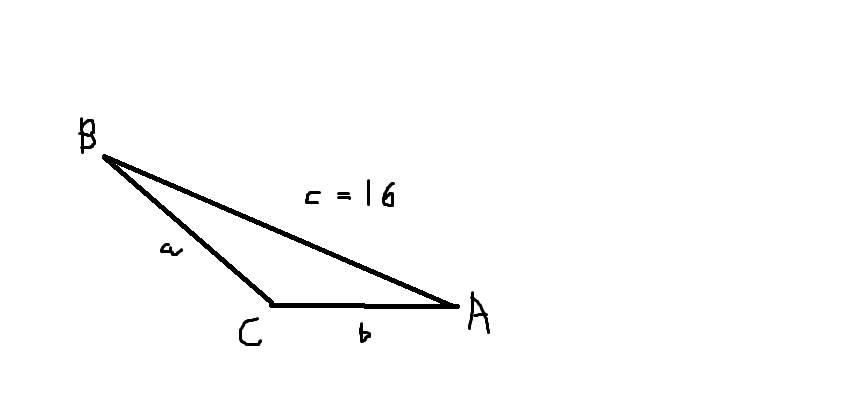
We can get the value of side A and B by using the "Law of Sines",
First, we must convert the radian value to degree value.
To convert radian value to degree value,
Multiply it by
since Angle
Angle
and Angle
Angle
using the law of sines,
using algebraic technique we get,
we use again the "Law of Sines", since "Pythagorean Theorem" doesn't work on Non-Right Triangles,
since angle
Angle
Angle
Applying again the Law of Sines to get the value of side of
Applying algebraic technique, we get,
Side
Hence, we get:
Side
Tip on Trigonometry:
Pythagorean Theorem is only reliable in solving right triangles, while Law of Sines and Cosines works in almost any triangles
:)

