A triangle has sides A, B, and C. The angle between sides A and B is #(5pi)/12# and the angle between sides B and C is #pi/12#. If side B has a length of 21, what is the area of the triangle?
1 Answer
Mar 24, 2018
Explanation:
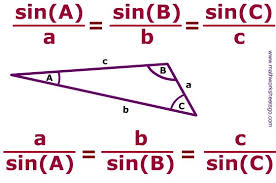
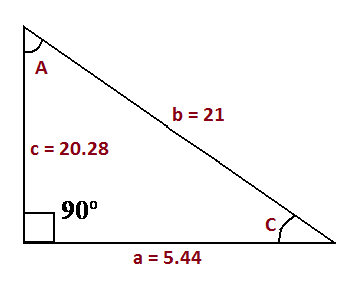
According to Law of Sines,
Area of Triangle " A_t = (1/2) a c = (1/2) * 5.44 * 20.28 = 55.16 "sq units"#
