A triangle has sides A, B, and C. The angle between sides A and B is #(5pi)/12# and the angle between sides B and C is #pi/12#. If side B has a length of 9, what is the area of the triangle?
1 Answer
Oct 10, 2016
Explanation:
We can compute the third angle with the other two angles as the sum of the angles in a triangle is
#"Third angle"=180-(75+15)=180-90=90^circ#
As the triangle contains a
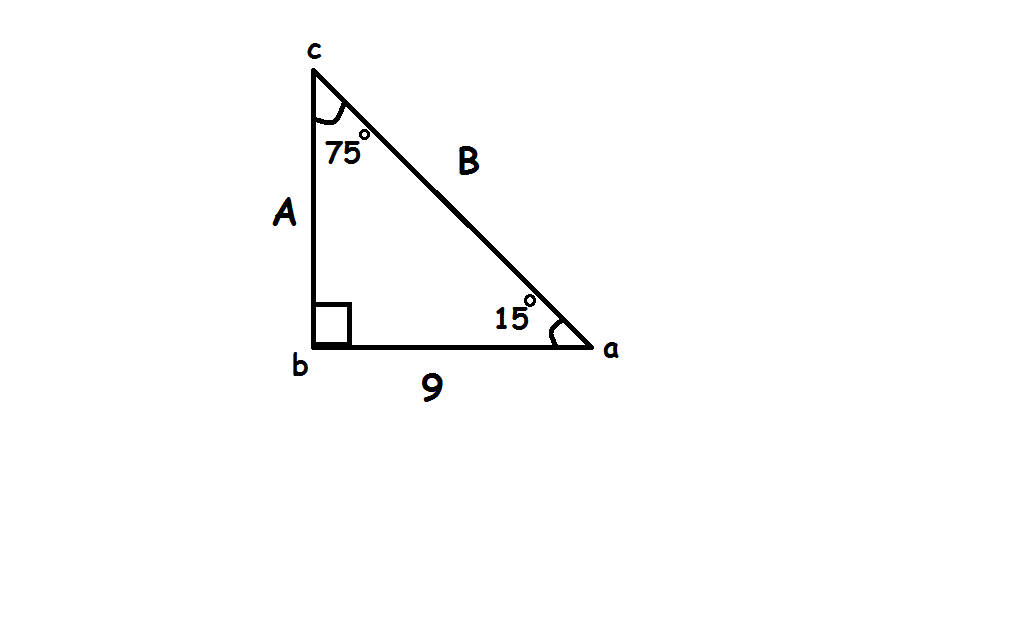
We need to find one more side to find the area of the triangle
So, we can use
#color(orange)(tan(theta)=("opposite") /(" hypotenuse")#
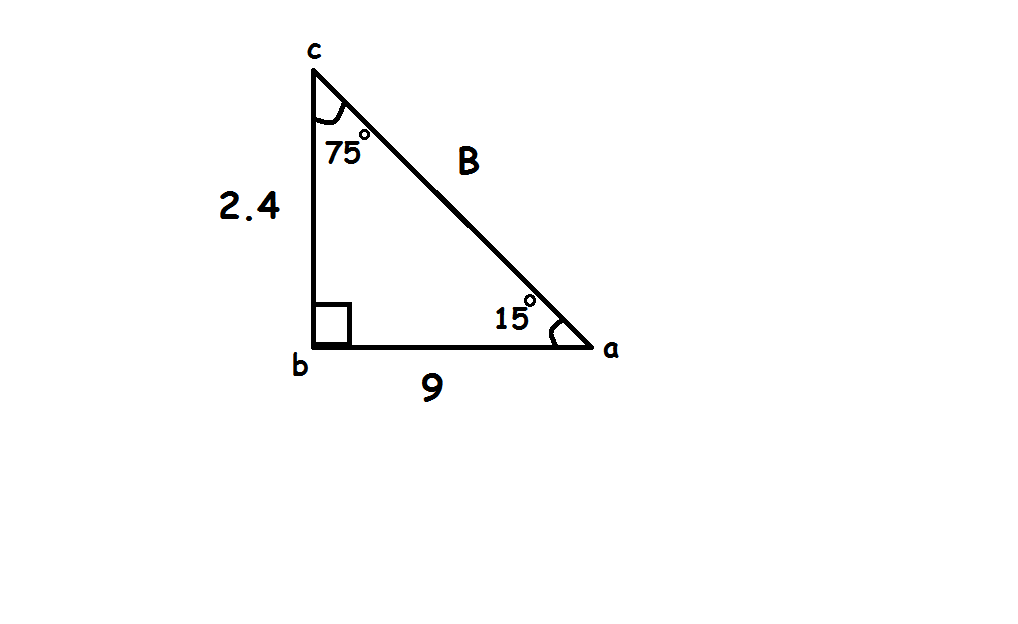
We can calculate the area of the triangle
#color(blue)("Area of triangle"=1/2*h*b#
Where,
#color(red)(h="height"=2.4#
#color(red)(b=base=9#

