A triangle has sides A, B, and C. The angle between sides A and B is #(5pi)/6# and the angle between sides B and C is #pi/12#. If side B has a length of 5, what is the area of the triangle?

Question

1842 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-22T19:33:36

#6.25# #units^2#

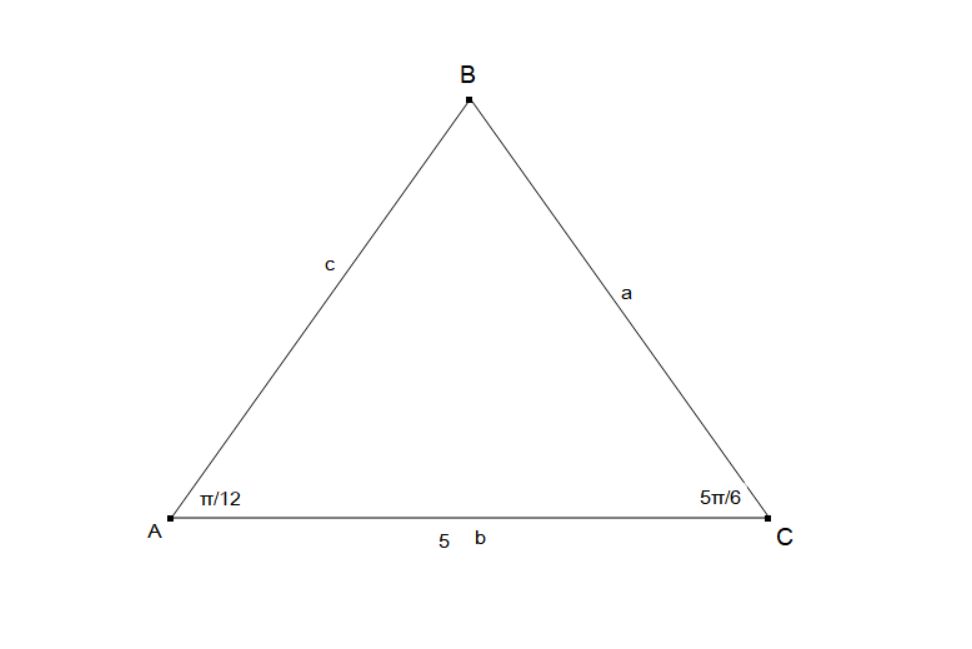
enter image source here

We first need to calculate the the third angle.

#B= pi -(pi/12 +(5pi)/6)=pi/12#

We can calculate the length of side #a# using the Sine Rule:

#sin(A)/a=sin(B)/b=sin(C)/c#

#sin(pi/12)/a=sin(pi/12)/5=>a = (5sin(pi/12))/(sin(pi/12))=5#

We can find the altitude using:

#a * sin(C)#

Since area is #1/2xxbase xxheight#

We have:

#1/2*5*5*sin((5pi)/6)= 6.25# #units^2#

Answer 2 · 2017-10-23T14:40:32

#color(magenta)(6.249 units^2# to the nearest 3 decimal places

#:.(cancel(5pi)^color(magenta)5)/cancel6^color(magenta)1xx180^color(magenta)30/cancelpi^color(magenta)1=150^@= angle# between sides A and B

#:.(cancelpi^color(magenta)1)/cancel12^color(magenta)1xxcancel180^color(magenta)15/cancelpi^color(magenta)1=15^@= angle# between sides B and C

#:.180-(150+15)=15^@= angle# between sides A and C

The #triangle#= a isoceles triangle

Area of #triangle=# #1/2# base# xx# height

#:.#Base#=C=C/(sin 150^@)=5/(sin15^@)#

multiply both sides by #sin150^@#

#:.C=(5xxsin150^@)/(sin15^@)#

#:.C=(5xx0.5)/0.258819045#

#:.C=(2.5)/0.258819045#

#color(magenta)(C=9.659=Base#

Perpendicular # heightcolor(magenta)(= D#

#:.D/5=Sin15^@#

multiply both sides by #5#

#:.D=5xxsin15^@#

#:.D=5xx0.258819045#

#:.color(magenta)(D=1.294 units# perpendicular height

#:.#The area of the triangle#color(magenta)(=1/2xx9.659xx1.294=6.249 units^2# to the nearest 3 decimal places