Question

A triangle has sides A, B, and C. The angle between sides A and B is `(5pi)/6`. If side C has a length of `5` and the angle between sides B and C is `pi/12`, what are the lengths of sides A and B?

Answer 1

`A = B = 2.59`

Explanation:

Given two angles, the third one in a triangle is fixed. In this case it is `pi – 10pi/12 – pi/12 = pi/12`. We have a very flat isosceles triangle.

We now have three angles and a side, and can calculate the other sides using the Law of Sines.

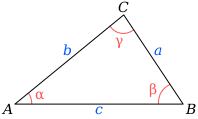
The Law of Sines (or Sine Rule) is very useful for solving triangles:
`a/sin alpha = b/sin beta= c/sin gamma`

Where: a, b and c are sides. `alpha`, `beta` and `gamma` are angles. (Side a faces angle `alpha` (or A), side b faces angle `beta` (or B) and side c faces angle `gamma` (or C).

And it says that: When we divide side a by the sine of angle `alpha`
it is equal to side b divided by the sine of angle `beta`,
and also equal to side c divided by the sine of angle `gamma`.
https://www.mathsisfun.com/algebra/trig-sine-law.html

For the given problem values: `C = 5, c = 5pi/6, a = b = pi/12`
`5/sin (5pi/6) = A/(sin(pi/12)) = B/(sin(pi/12))` (A = B)

`A = B = (sin(pi/12)) xx 5/sin (5pi/6) = 0.259 xx 10 = 2.59`