A triangle has sides A, B, and C. The angle between sides A and B is (pi)/2 and the angle between sides B and C is pi/12. If side B has a length of 22, what is the area of the triangle?
1 Answer
Mar 26, 2018
Area of the rt. triangle
Explanation:
Applying Law of sines,
It's a right triangle with
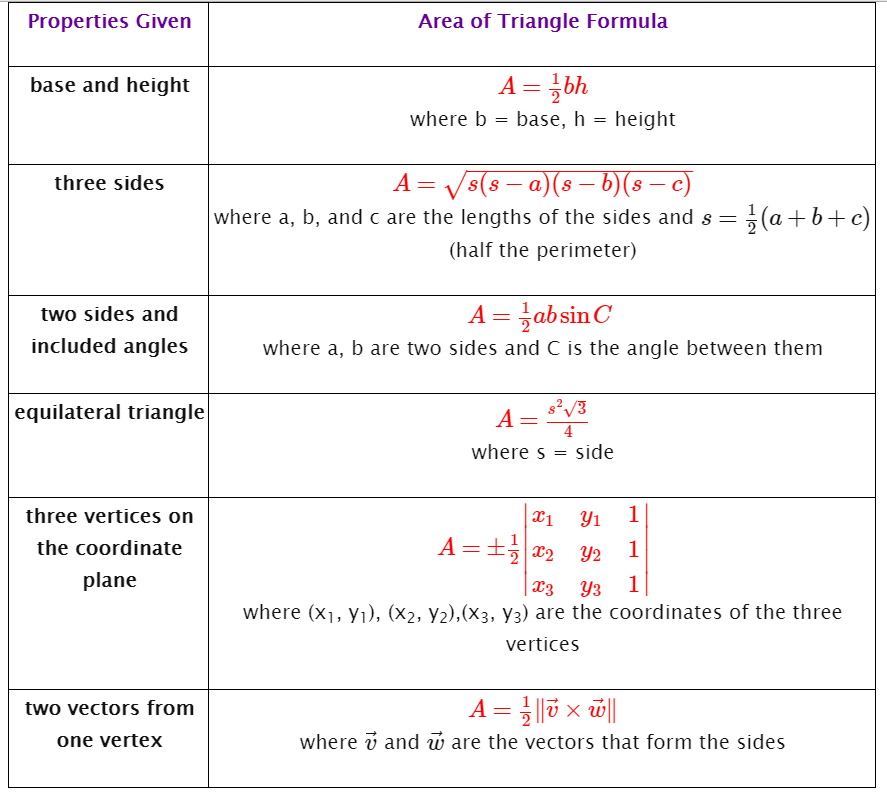 https://www.onlinemathlearning.com/area-triangle.html
https://www.onlinemathlearning.com/area-triangle.html
Hence area of the rt. triangle
