A triangle has sides A, B, and C. The angle between sides A and B is #(pi)/2# and the angle between sides B and C is #pi/12#. If side B has a length of 5, what is the area of the triangle?
1 Answer
Explanation:
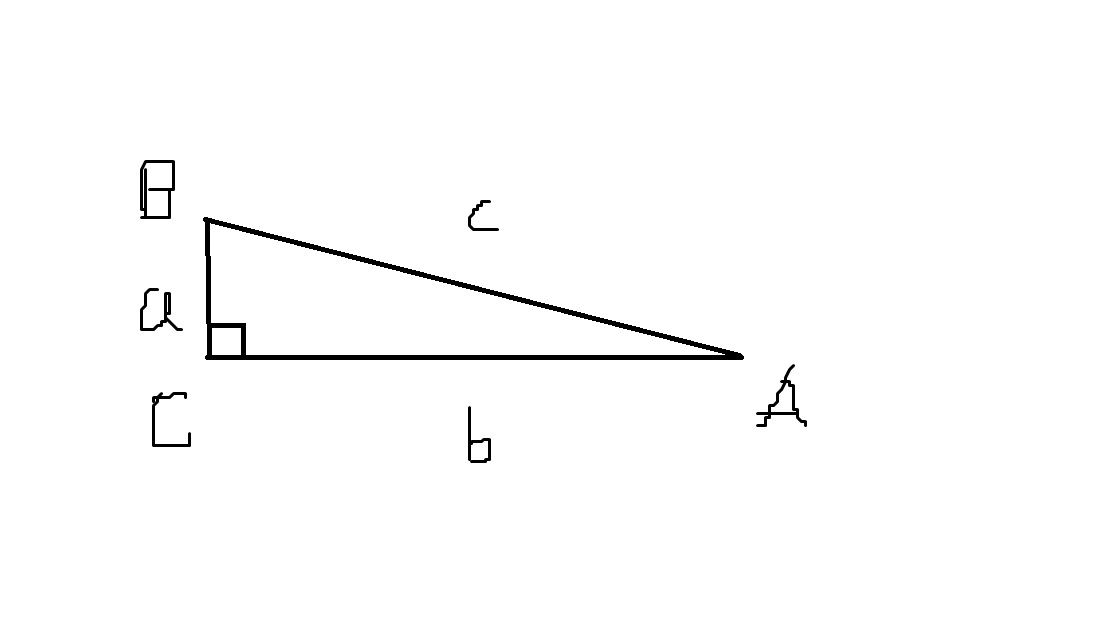
NOTE: Diagram drawn not to scale
Sorry for my bad drawing :D
Angles in Uppercase Letters (A, B, C)
Sides in Lowercase Letters (a, b, c)
Angle
Angle
to convert radian values to degrees, we simply multiply it by
Angle
Angle
Angle
Angle
Side
we must get the value of Side
we can use trigonometric functions to get the value of side of the triangle and apply algebraic techniques to find the value of
Since the formula for Area of Triangle is,
where
Plugging All Variables,

