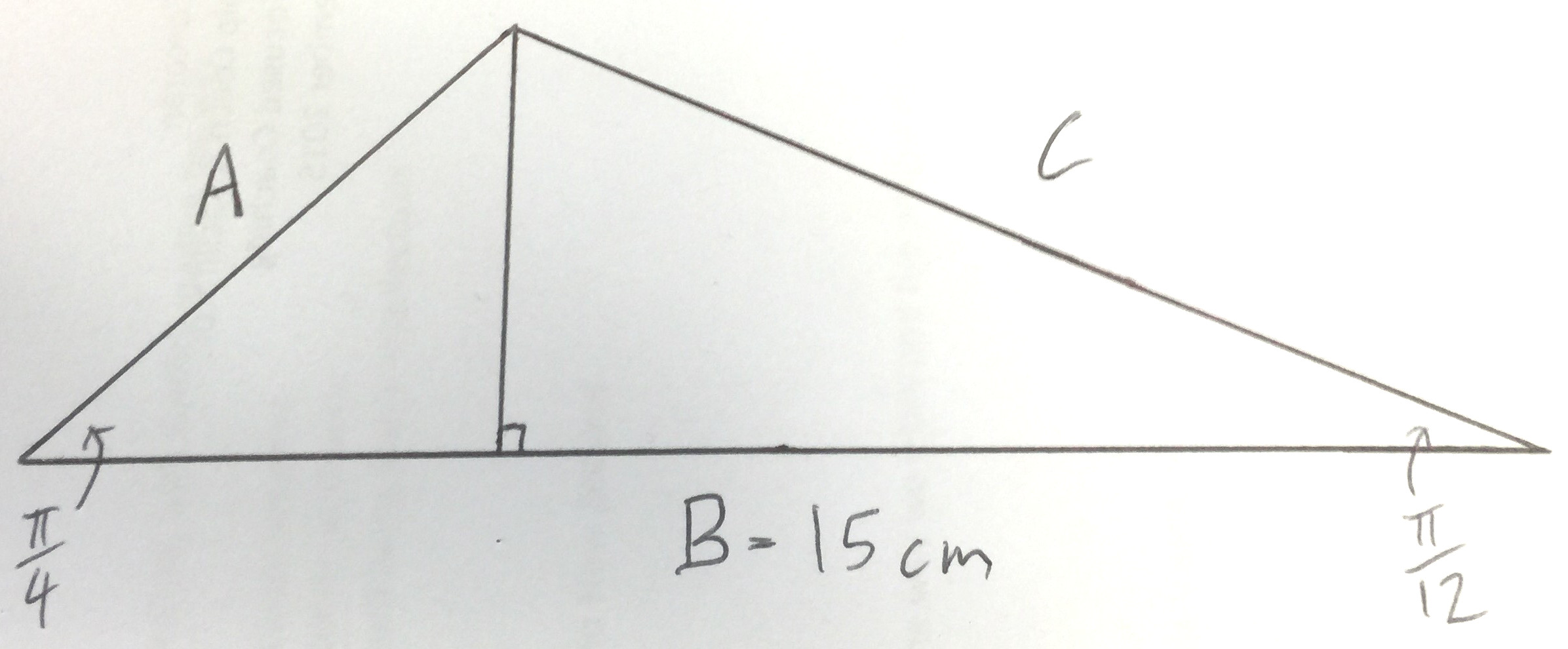
A triangle has sides A, B, and C. The angle between sides A and B is #pi/4# and the angle between sides B and C is #pi/12#. If side B has a length of 15, what is the area of the triangle?
1 Answer
The area of a triangle is given by
Explanation:
Drawing a clear diagram is essential for this kind of problem. Mine is not perfectly to scale, but it allows me to have clear in my own mind what information I have and what I'm trying to achieve.
(I've placed the image at the bottom of the page because the formatting works better that way.)
We know that the area of a triangle is given by:
We already know that the base is
We could use sine rule or cosine rule in the main triangle (they work in all triangles, not just right-angled ones), but we still need a little more information.
In radians, the angles in a triangle add up to
Now we can use the sine rule to find the length of
(for our purposes here, lowercase letters represent angles and uppercase represent sides, though the convention is usually the other way around)
Now that we know the length of
Now we know the base and height of the triangle, we can calculate its area: