A triangle has sides A, B, and C. The angle between sides A and B is #(pi)/6# and the angle between sides B and C is #pi/6#. If side B has a length of 3, what is the area of the triangle?
1 Answer
Dec 6, 2016
Explanation:
As can be seen from the image below, the given triangle can be split into 2 triangles with angles:
This is the ratios for one of that standard trigonometric triangles
we can see that the height of the original triangle must be
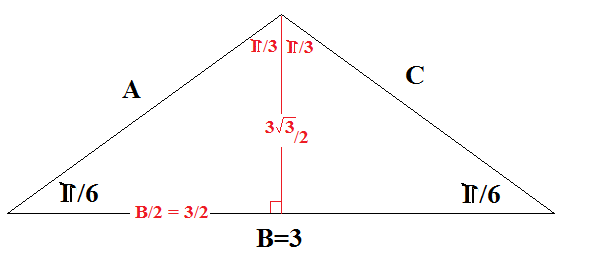
and the triangle's area will be:
