A triangle has two corners with angles of # pi / 12 # and # (7 pi )/ 8 #. If one side of the triangle has a length of #13 #, what is the largest possible area of the triangle?

Question

1496 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-07T02:54:40

Largest possible area of the triangle is #color(blue)(A_t = 64.1194)#

Given #/_A = (7pi)/8, /_B = pi /12#

#/_C = pi - (7pi)/8 - pi/12 = pi / 24#

Smallest angle is #/_C = pi/24#

enter image source here

To get the largest area of the triangle possible, smallest angle should correspond to the given length 13.

#i.e c = 13#

We know,
#a / sin A = b / sin B = c / sin C#

Hence,
#a / sin ((7pi)/8) = b / sin (pi/12) = 13 / sin (pi / 24)#

#a = (13 * sin ((7pi)/8)) / sin (pi/24) = 38.1141#

#b = (13 * sin (pi/12)) / sin (pi / 24) = 25.7776#

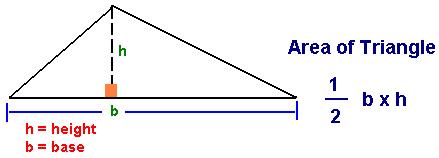
Area of triangle #A_t # =1/2 . Base . Height

Base #a = 38.1141#

Height #h = c sin (/_B) = 13 * sin (pi / 12) = 3.3646#

#A_t = (1/2) * 38.1141 * 3.3646 = color(blue)(64.1194)#

Largest possible area of the triangle is #color(blue)(A_t = 64.1194)#

Verification :

#**A_t** = (1/2) * a * b sin C = (1/2) * 38.1141 * 25.7776 * sin (pi/24) =**64.1194**#