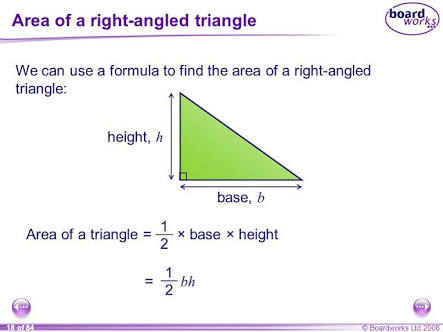
A triangle has two corners with angles of # pi / 2 # and # ( pi )/ 8 #. If one side of the triangle has a length of #3 #, what is the largest possible area of the triangle?

Question

1287 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-27T16:11:35

Largest possible area of the triangle is

#A_t = color(indigo)(10.864# sq units

#hat A = pi/2, hat B = pi/8#

Third angle #hat C = pi - pi / 8 /- pi /2 = (3pi)/8#

To get largest area, side with length 3 should correspond to the smallest angle #pi/8#

Applying law of sines,

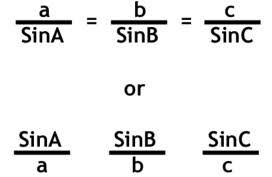
enter image source here

#3 / sin (pi/8) = b / sin (pi/2) = c / sin (3pi)/8#

#b = (3 * sin (pi/2)) / sin (pi/8) = 7.8394#

Area of the tan be arrived at by using the formula

#A_t = (1/2) a b sin C = (1/2) * 3 * 7.8394 * sin ((3pi)/8) = 10.864# sq units.

Alternatively,

#c = (3 * sin ((3pi)/8)) / sin (pi / 8) = 7.2426#

Since it’s a right triangle,

enter image source here

#A_t = (1/2) a c = (1/2) 3 * 7.2426 = 10.864#