A wooden crate has a mass of 780g, a height of 6.4 cm, a width of 8.7 cm, and a length of 52cm. What is the density of the crate?
1 Answer
Explanation:
As you know, density is defined as mass per unit of volume
#color(blue)("density" = "mass"/"unit of volume")#
This means that every time a problem asks you to calculate a substance's density, your goal will basically be to determine the mass of one unit of volume of that substance.
In your case, the dimensions of the wooden crate are given to you in centimeters, By the time you'll finish determining the volume of the crate, you'll end up with cubic centimeters.
This means that must determine the mass of
So, you can think of your wooden crate as being a rectangular prism that has
- a height of
#"6.4 cm"# - a width of
#"8.7 cm"# - a length of
#"52 cm"#
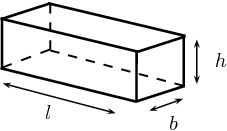
As you know, the volume of a rectangular prism is given by the formula
#color(blue)(V = l xx w xx h)" "# , where
Plug in your values to get
#V = "52 cm" xx "8.7 cm" xx "6.4 cm"#
#V = "2895.4 cm"^3#
Now, you know that this crate has a mass of
#1 color(red)(cancel(color(black)("cm"^3))) * "780 g"/(2895.4color(red)(cancel(color(black)("cm"^3)))) = "0.2694 g"#
This means that the density of the wooden crate will be
#rho = "0.2694 g"/"1 cm"^3 = color(green)("0.27 g/cm"^3)#
The answer is rounded to two sig figs.

