According to the molecular orbital theory, what is the bond order in #B_2^+#?
1 Answer
Boron atom is atomic number
The
where
#sigma^"*"# indicates an antibonding#sigma# (sigma) MO, and#sigma# is the bonding MO.
The antibonding MO is higher in energy because it has one more node than the corresponding bonding MO, and thus, the electrons are closer together (having less room to be), and repel each other more (increasing the destabilizing electron repulsion energy).
Analogous atomic orbital combinations for the
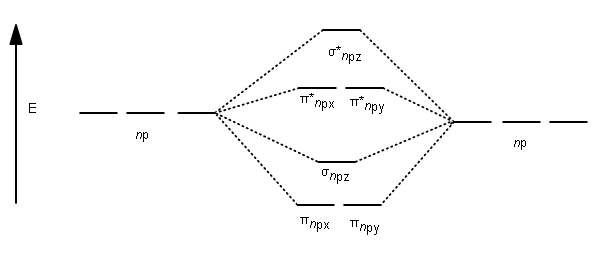
For the homonuclear diatomic molecules
Filling the molecular orbitals:
- The first four electrons fill the
#sigma_(1s)# and#sigma_(1s)^"*"# MOs. - The second four electrons fill the
#sigma_(2s)# and#sigma_(2s)^"*"# MOs. - The last two electrons singly occupy the
#pi_(2p_x)# and#pi_(2p_y)# MOs.
The bond order for
#"BO" = 1/2("Bonding electrons - Antibonding electrons")#
#= 1/2[(2 + 2 + 1 + 1) - (2 + 2)]#
#= 1/2(2) = 1#
That is, we expect boron to form this compound with itself:
#:"B"-"B":#
However, since you asked for
So,

