Question

An object, previously at rest, slides `12 m` down a ramp, with an incline of `pi/8`, and then slides horizontally on the floor for another `3 m`. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?

Answer 1

The coefficient of kinetic friction will be 0.326

Explanation:

This problem is most easily done by conservation of energy.
Two energy forms are involved:

A change in gravitational potential energy: `mgh`

Frictional heating: `muF_NDelta d_1+muF_NDeltad_2`

where `Deltad_1` is the distance the object slides along the ramp, and `Deltad_2` is the distance is slides along the horizontal surface.

Before we can continue, we need to be aware of a couple of complications

We must express `h` (the height the object descends) in terms of `Deltad_1` (its displacement along the ramp).

`h=Deltad_1sin(pi/8)`

Also, we must note that the normal force on an incline is not equal to mg, but to `mgcostheta`, where `theta=pi/8` in this case.

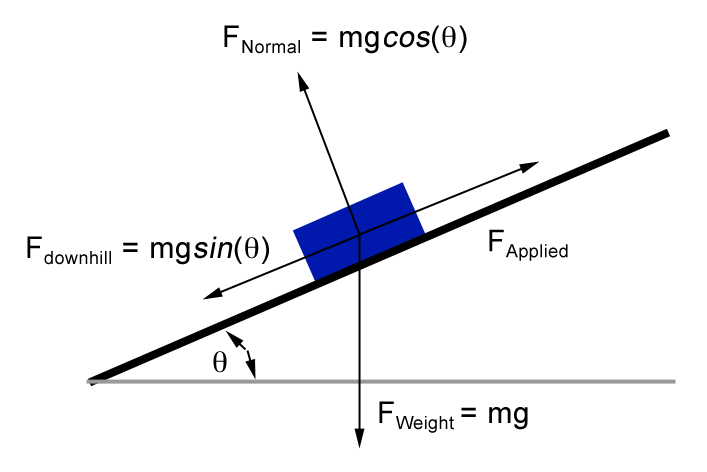
With all that looked after, our equation becomes

`-mgDeltad_1sin(pi/8)+mumgcos(pi/8)Deltad_1+mumgDeltad_2=0`

(The first term is negative because the potential energy decreases.)

Notice that we can divide every term by mg, (including the right side of the equation)

So, inserting 12 m for `Deltad_1` and 3m for `Deltad_2` we get:

`-12(0.383)+(mu)(0.924)12+mu(3)=0`

`-4.60+11.09mu+3mu=0`

`14.09mu=4.60`

`mu=0.326`