An object, previously at rest, slides #3 m# down a ramp, with an incline of #pi/6 #, and then slides horizontally on the floor for another #8 m#. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?
1 Answer
Use conservation of energy to tackle this problem, and you get
Details below...
Explanation:
Conservation of energy is best for doing this problem.
Here, there are two forms of energy that must be considered - potential energy and frictional heating. The fact that the object starts at rest, and ends the problem at rest means we can ignore kinetic energy changes during the motion!
Conservation of energy will involve three terms
Note I have two terms for frictional heating. This is necessary because the normal force changes when the object goes from ramp to floor, and so, the force of friction also changes, (although the coefficient of friction remains the same).
Let
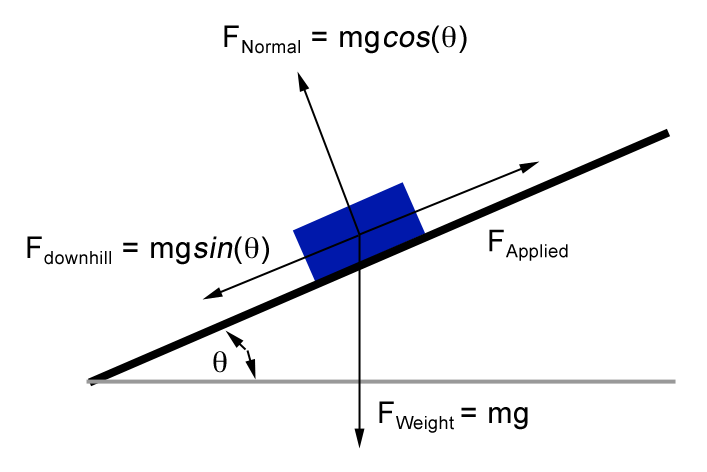
Then, the equation is
where the height the object descends on the ramp is
Getting the numbers in place, after first canelling "mg" from every term
(-1.5) + 10.6mu=0#

