An object, previously at rest, slides #4 m# down a ramp, with an incline of #pi/3 #, and then slides horizontally on the floor for another #9 m#. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?
1 Answer
Explanation:
Since the object begins from rest at the top of the ramp and comes to rest on the floor below, we know that all of the gravitational potential energy originally possessed by the object is lost to friction by the time it comes to a stop.
Therefore, we know that the work done by friction, or the energy lost to friction, is equal to the object's gravitational potential energy at the top of the ramp.
Gravitational potential energy:
#U_g=mgh#
Work done by kinetic friction:
#W_f=f_k*d#
Therefore, we have:
#=>mgh=W_f#
#=>color(blue)(mgh=f_k*d)#
It is necessary to break up the right side into a sum of the work done by friction while the object is on the ramp as well as when it is sliding across the floor. Let's call the distance down the ramp
#mgh=W_(f" total")#
#mgh=W_(f " ramp")+W_(f" floor")#
#=>color(blue)(mgh=f_k*r+f_k*d)#
We have the following information:
#|->r=4"m"# #|->theta=pi/3# #|->d=9"m"#
Diagram:
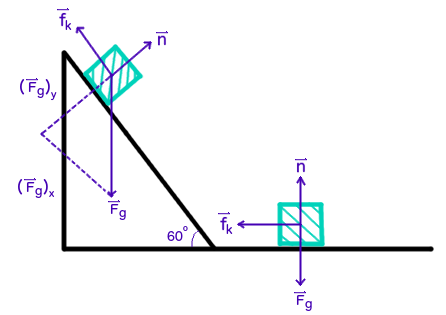
where
#vecn# is the normal force,#vecf_k# is the force of kinetic friction, and#F_g# is the force of gravity, decomposed into its parallel (x) and perpendicular (y) components.
We can find
#sin(theta)="opposite"/"hypotenuse"#
#=>sin(pi/3)=h/4#
#=>h=4sin(pi/3)#
Now let's take inventory of the forces acting on the object while on the ramp and on the floor.
Ramp:
#color(blue)(sumF_x=F_gsin(theta)-f_k=ma_x)#
#color(blue)(sumF_y=n-F_gcos(theta)=0)#
- Note that there is no net perpendicular (y) force and therefore no acceleration in that direction (dynamic equilibrium).
We can solve for n:
#n=F_gcos(theta)#
#=mgcos(theta)#
Floor:
#color(darkblue)(sumF_x=-f_k=ma_x)#
#color(darkblue)(sumF_y=n-F_g=0)#
Again, we can solve for n, and we find that
Substituting back in...
#mgh=mu_kmgcos(theta)r+mu_kmgd#
#cancelcolor(darkblue)(m)cancelcolor(blue)(g)h=mu_kcancelcolor(darkblue)(m)cancelcolor(blue)(g)cos(theta)r+mu_kcancelcolor(darkblue)(m)cancelcolor(blue)(g)d#
#h=mu_kcos(theta)r+mu_kd#
Solve for
#h=mu_k(cos(theta)r+d)#
#color(blue)(mu_k=h/(cos(theta)r+d))#
And now, substituting in our known values:
#mu_k=(4sin(pi/3))/(4cos(pi/3)+9)#
#mu_k~~0.315#

