An object, previously at rest, slides #5 m# down a ramp, with an incline of #(pi)/6 #, and then slides horizontally on the floor for another #24 m#. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?
1 Answer
Explanation:
I've answered a similar question previously.
We are given the angle of incline, displacement of the object down the ramp, and displacement of the object between the bottom of the ramp and its stopping point. We can find the coefficient of kinetic friction using the work-energy theorem.
The first step is to draw a force diagram.
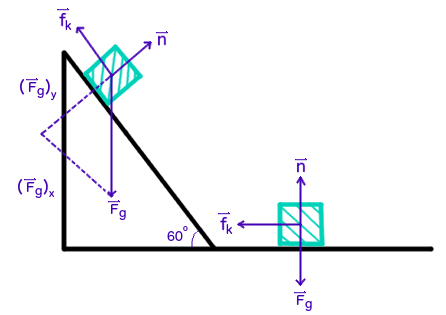
Where
When the object is at rest at the top of the ramp, it possesses only gravitational potential energy, given by
Work is defined as the mechanical transfer of energy. When the object comes to a stop on the floor, it no longer has either gravitational potential or kinetic energy, but by the Law of Conservation of Energy, we know that the energy had to go somewhere. In this case, if we treat friction as the only outside force energy can be lost to, that means that all of the potential energy stored in the object at the top of the ramp is accounted for in the work done by friction. In other words, the energy lost is equal to the work done by friction. This means that
Force of kinetic friction:
Work done by a constant force:
Note: In the work equation,
Note: I will use Δr for the ramp and Δs for the floor to avoid confusion.
The potential energy stored in the object at the top of the ramp is equal to the total work done by friction. This includes both that done on the ramp and the floor (the point where all of the potential energy has been converted is when the object comes to a stop on the floor).
The final height is
Let's cancel the negative.
Looking at our force diagram above, we can generate sum of forces statements for when the object is on the ramp and the floor.
Ramp:
(No acceleration in the
Therefore,
Floor:
Therefore,
For our potential energy, we will need to find
We now have:
Both the mass,
We can rearrange to solve for
Using our known values:
Hope that helps!

