An object with a mass of #4 kg# is on a plane with an incline of # - pi/8 #. If it takes #18 N# to start pushing the object down the plane and #5 N# to keep pushing it, what are the coefficients of static and kinetic friction?
1 Answer
I found
Explanation:
Have a look at the diagram:
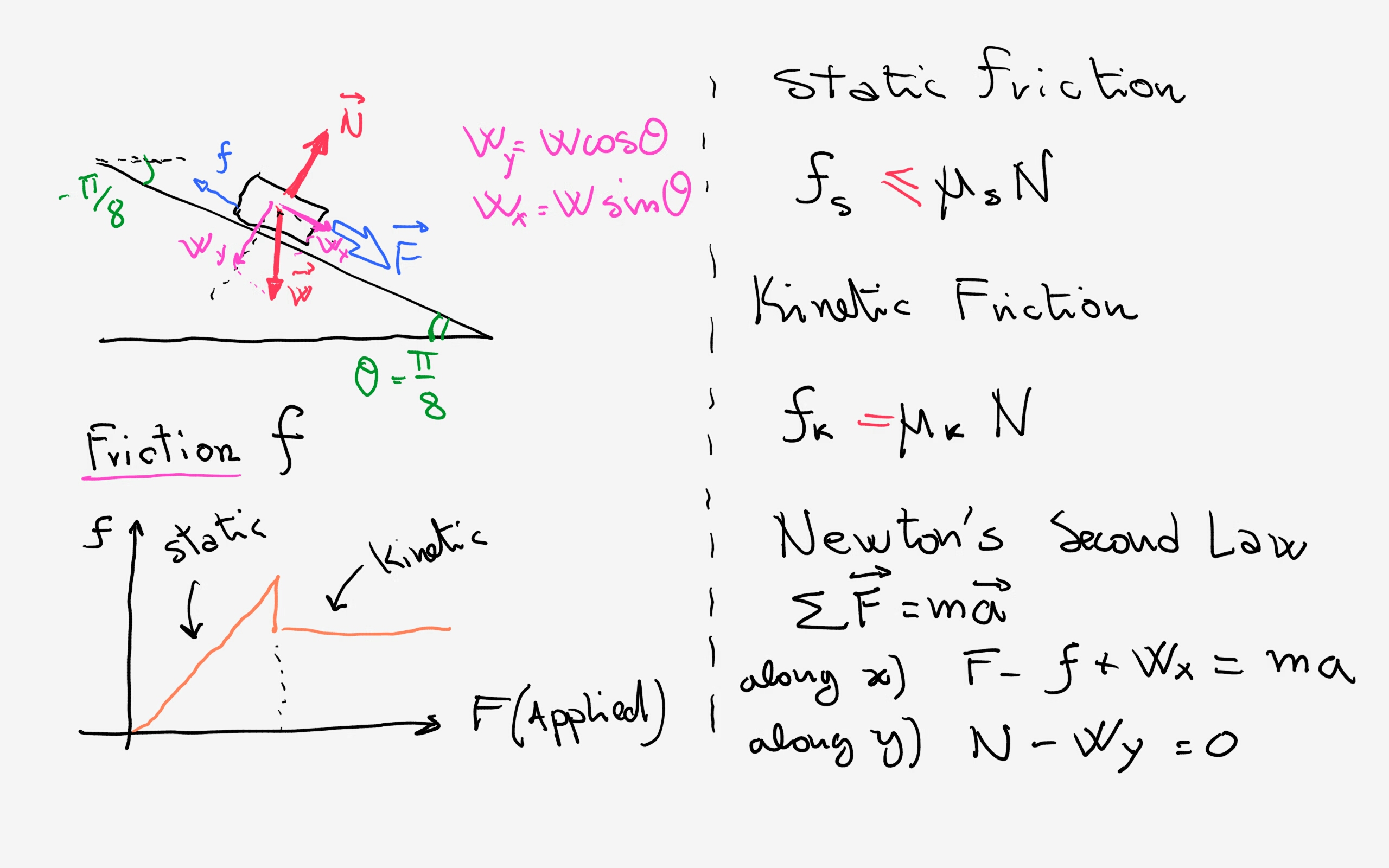
I assumed that the negative angle represents the downward inclination of the surface and transferred it as
With this convention for the angle and Newton's law:
Also:
Now:
1) Static Friction:
I consider the object still at rest but almost moving. Acceleration will be zero and we will be at maximum static friction where it will exactly be:
So, we use Newton's law along
2) Kinetic Friction:
From our graph of friction we can see that Kinetic friction will be almost constant and so:
Here we can assume that the object will move with constant velocity down the incline giving again zero acceleration. As before we get, using Newton's law along

