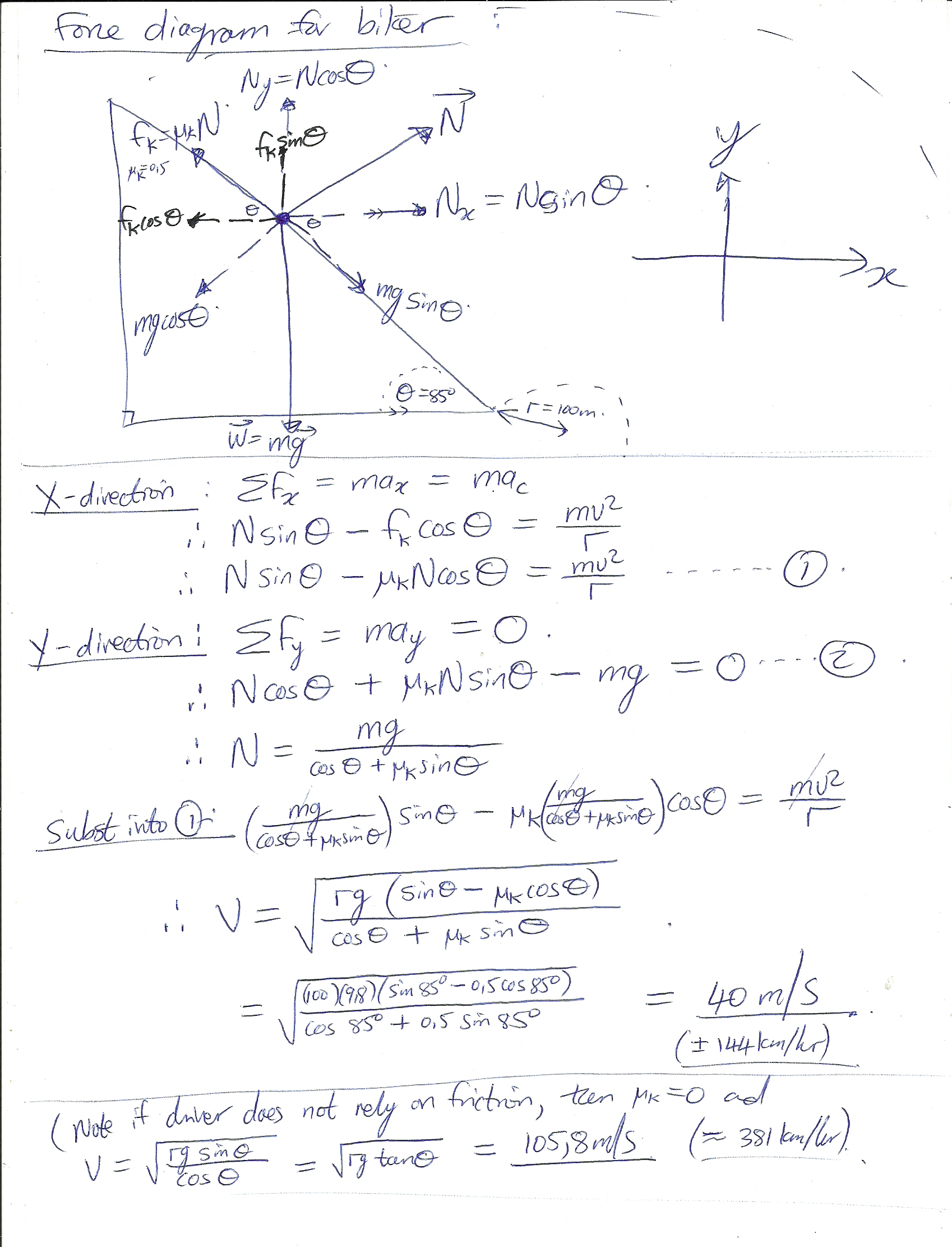
Application of mechanics - What minimum linear velocity is required by a racing driver to round a bend of radius 100m, inclined at angle 85 degrees to the horizontal, if the coefficient of kinetic friction between his tyres and the surface is 0,5? See ske
Nice application of mechanics to everyday life - See sketch in website link below of this date, latest updated image of bike rider on the corner, copied and pasted from a facebook post.
https://www.facebook.com/groups/199316916762808/

A nice application of physics to everyday life - long last since i posted one of these smile emoticon:)
There is an actual race track in America with a corner being an inclined plane (perhaps not quite as steep as the one in the photo).
Here's the problem -
Several contributors on the original facebook post i copied have debated as to whether or not it is actually possible to successfully negotiate such a steeply inclined plane. To answer the question from a physics point of view, perform the following calculation using reasonable values given:
Calculate the minimum linear velocity required by the racer to maintain his line through the corner if the horizontal radius of the corner is 100 m and the coefficient of kinetic friction between his tyres and the surface is 0,5. Assume the inclination angle between the horizontal and the inclined berm is 85 degrees as shown in the sketch.
Let us see if any of my past students can solve this one..... grin emoticon
Nice application of mechanics to everyday life - See sketch in website link below of this date, latest updated image of bike rider on the corner, copied and pasted from a facebook post.
https://www.facebook.com/groups/199316916762808/

A nice application of physics to everyday life - long last since i posted one of these smile emoticon:)
There is an actual race track in America with a corner being an inclined plane (perhaps not quite as steep as the one in the photo).
Here's the problem -
Several contributors on the original facebook post i copied have debated as to whether or not it is actually possible to successfully negotiate such a steeply inclined plane. To answer the question from a physics point of view, perform the following calculation using reasonable values given:
Calculate the minimum linear velocity required by the racer to maintain his line through the corner if the horizontal radius of the corner is 100 m and the coefficient of kinetic friction between his tyres and the surface is 0,5. Assume the inclination angle between the horizontal and the inclined berm is 85 degrees as shown in the sketch.
Let us see if any of my past students can solve this one..... grin emoticon
1 Answer
Explanation:
The horizontal component of the normal force provides the required centripetal force to maintain uniform circular motion.
The full mathematical analysis is given in the attachment below.