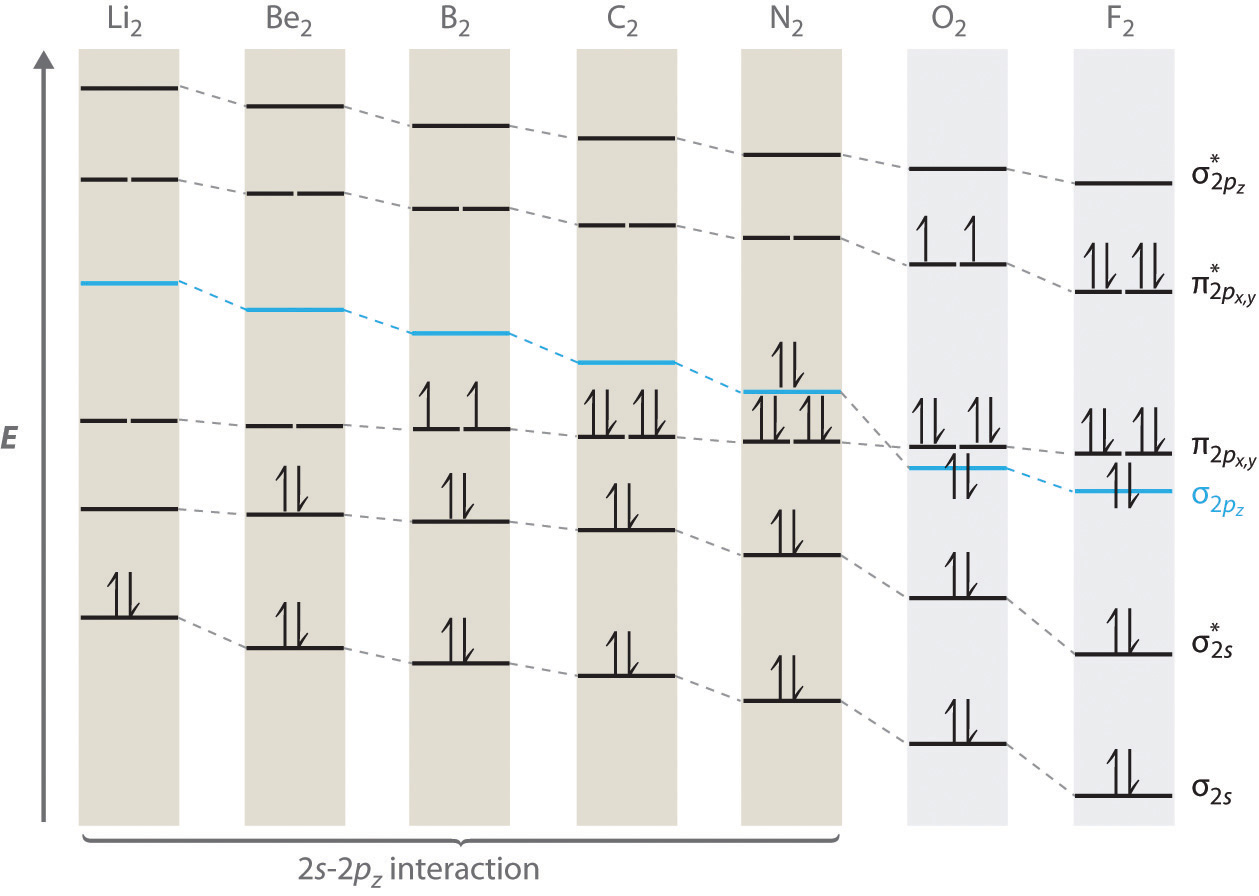
Recall that paramagnetic means it contains at least one unpaired electron and diamagnetic is the lack thereof.
"O"_2 is paramagnetic, with one electron each in its pi_(2p_x)^"*" and pi_(2p_y)^"*" antibonding molecular orbitals.
![]()
When we go back over to "N"_2, since "N" has one less electron than "O" in its atomic orbitals, "N"_2 has two less electrons than "O"_2 in its molecular orbitals.
Furthermore, going from "O"_2 to "N"_2 doesn't change the energy ordering for the pi_(2p_x)^"*" and pi_(2p_y)^"*" relative to the sigma_(2p_z) or pi_(2p_x) or pi_(2p_y), so this assumption is valid.
That means "N"_2 is diamagnetic, with no unpaired electrons.
In fact, its highest energy occupied molecular orbital (HOMO) is its sigma_(2p_z) bonding orbital, which currently contains two electrons.
 )
)
(Due to orbital mixing effects between the sigma_(2s) and sigma_(2p_z) from "Li"_2 to "N"_2, the sigma_(2p_z) is higher in energy relative to if the effects were not present, and the sigma_(2s) is lower in energy instead. "N"_2 and "O"_2 mark the border-crossing for when these effects are not significant; that is, when the sigma_(2s) and sigma_(2p_z) are too far in energy to interact.)
"N"_2^(+) therefore involves the removal of one sigma_(2p_z) electron.
Thus, "N"_2^(+) has a paramagnetic configuration due to the unpaired sigma_(2p_z) electron.
Think about it; if you lose an electron in a bonding molecular orbital, does the bond get weaker or stronger? "N"_2^(+) has less bonding character than "N"_2, which means it is less thermodynamically stable.
Does that mean it's a weaker bond? You should be able to figure this out from here.
 )
) 
