Are non-valence electrons represented in a Lewis dot diagram?

1 Answer
Shivangi Mangotra
Nov 2, 2014

Only valence electrons are represented in Lewis dot diagrams. Never draw electrons other than valence electrons.
For example,
CHLORINE
The electronic configuration for chlorine is,
E.C :- K=2, L=8,M=7
The lewis dot diagram for chlorine is,
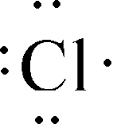
!enter image source here
In the electron configuration above the last shell that is the M shell has 7 electrons in it and the diagram above also 7 electrons are drawn.

Related questions
See all questions in Lewis Dot Diagram
Impact of this question
7244 views around the world
You can reuse this answer
Creative Commons License