At 120.0°C, the pressure of a sample of nitrogen is 1.07 atm. What will the pressure be at 205°C, assuming constant volume?
1 Answer
Explanation:
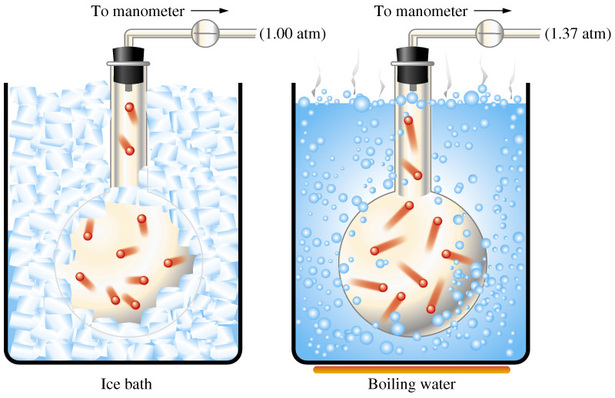
The important thing to remember about a gas kept at constant volume is that its pressure and its temperature are directly proportional, assuming of course that the number of moles of gas are constant as well.
So, when volume and number of moles are kept constant, pressure and temperature have a direct relationship - this is known as Gay Lussac's Law.
 http://ouitschem.weebly.com/gas-laws.html
http://ouitschem.weebly.com/gas-laws.html
Simply put, when temperature increases, pressure increases. Likewise, when temperature decreases, pressure decreases as well.
In your case, the temperature of the gas increases from
Mathematically, Gay Lussac's Law is expressed like this
color(blue)(P_1/T_1 = P_2/T_2)" " , where
Now, it is of the utmost importance that you do not forget to convert the temperature from degrees Celsius to Kelvin!
In fact, the temperature must be expressed in Kelvin regardless of which gas law you're using.
So, plug in your values and solve for
P_1/T_1 = P_2/T_2 implies P_2 = T_2/T_1 * P_1
P_2 = ( (273.15 + 205)color(red)(cancel(color(black)("K"))))/((273.15 + 120.0)color(red)(cancel(color(black)("K")))) * "1.07 atm" = "1.4238 atm"
Rounded to three sig figs, the number of sig figs you have for the second temperature of the gas, the answer will be
P_2 = color(green)("1.42 atm")

