Can I get some help please? Thanks!
2 Answers
1086 mm Hg
Explanation:
Using the slope method
The change in pressure per degree C
The change in pressure per degree C second interval
# 40^o C - 20^oC = 20^oC
The change in pressure per degree C third interval
The change in pressure per degree C fourth interval
960- 880 = 80/30 = (2.6mm Hg)/1^oC #
averaging the change in pressure for the four intervals
The change in temperature 150-100 = 50 so
Adding this change in pressure to the value of 960 gives
960 + 126 = 1086 mmHg.
this is an approximate value as the the intervals do not give a perfect straight line slope.
I get
Explanation:
I would use Excel or a graphing calculator to plot a graph of
I don’t have a graphing calculator, so I plotted the data in Excel.
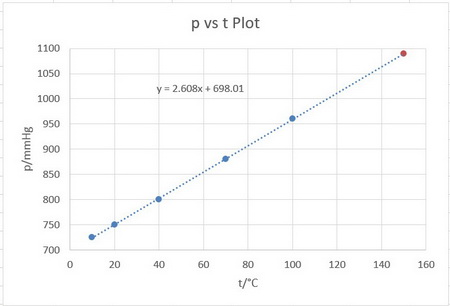
Excel told me that the equation of the best-fit line was
Substituting

