Can someone help me understand orbitals??
2 Answers
orbitals are the area of mathematical probability of finding an electron. They are based on Schondenger's wave equations.
Explanation:
Orbitals define the area we fhere it is likely ( based on the quantum mechanics ) of finding an electron
The simplest type of orbital is called an s orbital. It is a roughly spherical shape (very fuzzy) around the atom. There is one s orbital at each energy level on the periodic table. The electrons do not "orbit" around the atom at a set distance or direction. The uncertainty principle states that it is impossible to know both where an electron presently is and the direction it is traveling.
The first energy level ( Hydrogen and Helium) has only 1 s orbital
The second energy level has both a 1 s orbital and 3 p orbitals. (px, py, and pz)
the p orbitals having a more complicated shape and equation require more energy for an electron to occupy this probability locus.
The p orbitals are shaped generally like a 3d figure eight.
Again the borders of these p orbitals are not precise or sharp, it is a probability of finding the electrons there. ( note the exclusion principle says that no two electrons can occupy the exact same space so only two electrons one with a + spin and one with a - spin can occupy an orbital
The third energy level has three types of orbitals 1 s 3 p and 5 d's
The d electrons orbitals require more energy to occupy than the s or the p orbitals so much so that the 3d orbitals are filled by electrons in the fourth level of the periodic table.
In terms of filling orbitals for electron configurations, there are two sets of ideas we should get to know:
- Quantum numbers (
#n,l,m_l,m_s# ) - Filling rules (Aufbau Principle, Hund's Rule, Pauli Exclusion Principle)
QUANTUM NUMBERS
Basically, quantum numbers give rise to a set of rules on how we think electrons ought to behave. They allow us to describe where an electron is in space, and what its orientation is.
Recall the following:
#n# is the principal quantum number, which is the energy level. It can be#1, 2, 3, . . . # , and it is the number in front of the orbital name.#l# is the angular momentum quantum number, which tells you the shape of the orbital.#l = 0, 1, 2, . . . , n - 1# , and each#l# corresponds to an#s,p,d,f,g, . . . # orbital shape (subshell).#m_l# is the magnetic quantum number, which tells you the orientation of an orbital. Each#m_l# corresponds to an orbital, and#m_l = {-l, -l+1, . . . , 0, . . . , l - 1, l}# , so there are#2l+1# orbitals in a subshell.#m_s# is the spin quantum number, and it can be#pm"1/2"# , telling you that the electron can be either spin-up (#+"1/2"# ) or down (#-"1/2"# ).
Knowing all four quantum numbers allows you to describe what is called the electron's quantum state.
FILLING "RULES"
From those quantum numbers comes the "rules" we constructed to help predict how electrons ought to fill orbitals.
- The Aufbau Principle states that electrons fill orbitals from the lowest to highest energy. As-stated, it should be this general.
The first few energy levels are
#1s,2s,2p,3s,3p# . Most elements are expected to proceed with the filling order as#4s,3d,4p,5s,4d,5p,6s,4f,5d,6p, . . . # . Visually,#n = 1, 2, 3, 4# look somewhat like this:
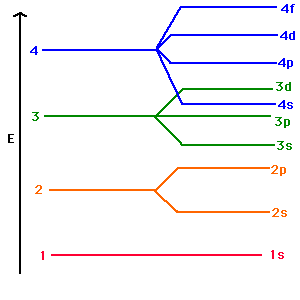
(Note that there are "exceptions" to the filling order, most notably being
#"Cr"# ,#"Mo"# ,#"Cu"# ,#"Ag"# , and#"Au"# , where one#ns# electron prefers to be in the#(n-1)d# orbitals.)
- Hund's Rule essentially states that electrons should fill orbitals in a way that as many electrons as possible are the same spin for the same
#l# .
That means filling each orbital one at a time, then doubling up later. So, the following are sequential steps on filling orbitals in the same subshell (specifically,
#p# orbitals):
#ul(color(white)(uarr darr))" "ul(color(white)(uarr darr))" "ul(color(white)(uarr darr))#
#=># #stackrel("Fill one by one first")overbrace(ul(color(blue)(uarr) color(white)(darr))" "ul(color(white)(uarr darr))" "ul(color(white)(uarr darr)))#
#=># #ul(uarr color(white)(darr))" "ul(color(blue)(uarr) color(white)(darr))" "ul(color(white)(uarr darr))#
#=># #ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(color(blue)(uarr) color(white)(darr))#
#=># #stackrel("Now, pair up electrons")overbrace(ul(uarr color(blue)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))#
#=># #ul(uarr darr)" "ul(uarr color(blue)(darr))" "ul(uarr color(white)(darr)#
#=># #ul(uarr darr)" "ul(uarr darr)" "ul(uarr color(blue)(darr)# An example of how Hund's Rule functions in choosing correct electron configurations:
This is NOT preferred (it's less stable):
#color(red)(ul(uarr darr)" "ul(color(white)(uarr darr))" "ul(color(white)(uarr darr)))# This IS preferred (it's more stable):
#color(blue)(ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(color(white)(uarr darr)))#
- The Pauli Exclusion Principle arises from the idea that no two electrons can share the same quantum state.
That means that two electrons in the same orbital must have opposite spins. In other words, two electrons of the same
#m_l# must have different#m_s# .This is OK:
#ul(uarr darr)# This is NOT:
#ul(color(red)(uarr uarr))# because electrons should be opposite spins within the same orbital.

