Question

Can you help me Transform from a polar to a rectangular equation?

`r=2sintheta+2costheta`

Answer 1

`(x-1)^2+(y-1)^2=2`

Explanation:

We use the following three definitions to convert between Cartesian and polar coordinates

`r:=sqrt (x^2+y^2)`

`x=rcostheta rArr costheta=x/r`

`y=rsintheta rArr sintheta=y/r`

Using these, we get the equation as

`r=(2y)/r+(2x)/r`

`rArrr^2=x^2+y^2=2x+2y`

`rArrx^2-2x+y^2-2y=0`

We now complete the square for both `x` and `y` to get the eqn in standard form

`(x-1)^2-1+(y-1)^2-1=0`

So finally,

`(x-1)^2+(y-1)^2=2`

Answer 2

Given:

`r=2sin(theta)+2cos(theta)`

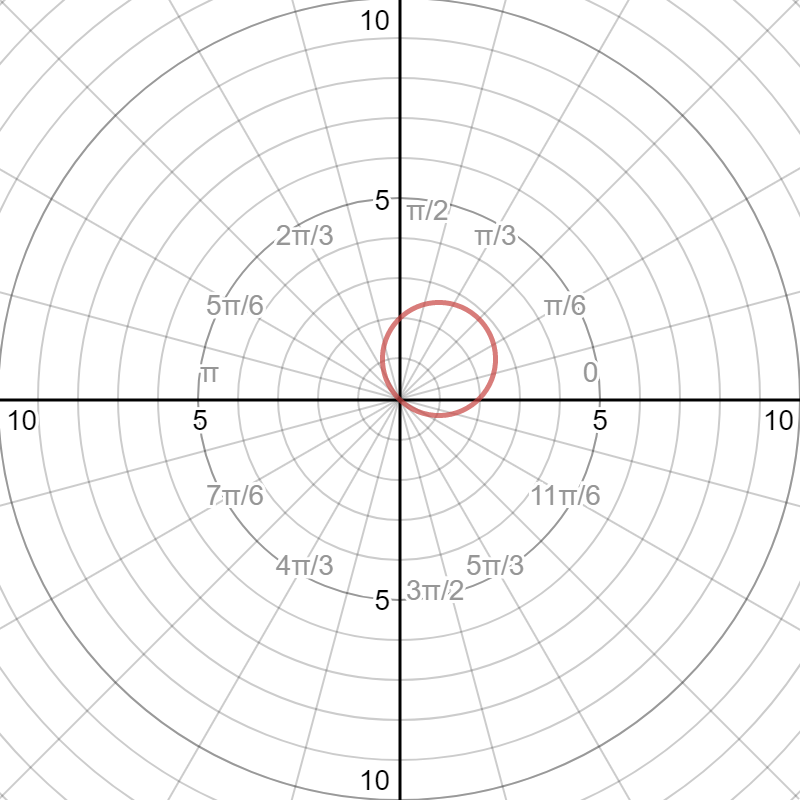
Please observe the graph of the polar equation:

Multiply both sides by `r`:

`r^2=2rsin(theta)+2rcos(theta)`

Substitute `r^2 = x^2+y^2, rsin(theta) = y, and rcos(theta) = x`:

`x^2+ y^2=2y+2x`

Subtract `2y+2x` from both sides:

`x^2-2x+ y^2-2y= 0`

Add `h^2+ k^2` to both dies:

`x^2-2x+h^2+ y^2-2y+k^2= h^2+k^2`

Using the pattern `(x - h)^2= x^2+2hx+h^2`, we observe that `h = 1`

`x^2-2x+1^2+ y^2-2y+k^2= 1^2+k^2`

Collapse the left side into a square:

`(x-1)^2+ y^2-2y+k^2= 1^2+k^2`

Using the pattern `(y - k)^2= y^2+2kx+k^2`, we observe that `k = 1`

`(x-1)^2+ y^2-2y+1^2= 1^2+1^2`

Collapse the left side into a square and combine like terms on the right:

`(x-1)^2+ (y-1)^2= 2`

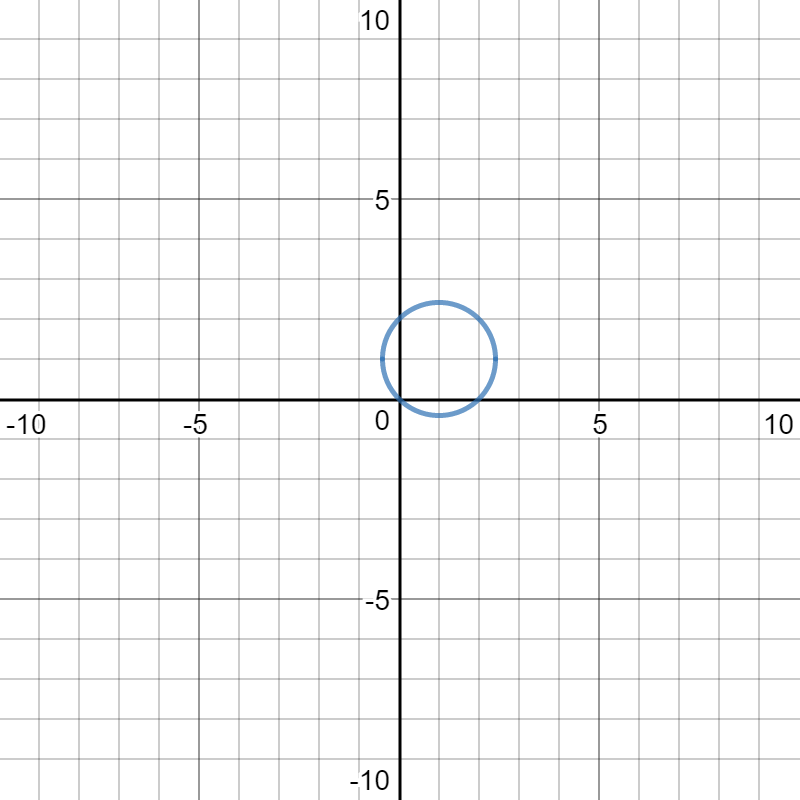
Write in standard form:

`(x-1)^2+ (y-1)^2= (sqrt2)^2`

This is a circle with its center at the point `(1,1)` and it radius, `r = sqrt2`:

Please observe that the graph is identical to the original equation: