Question

Consider a system of three point charges ont the x axis. Charge 1 is at x=0, charge 2 is at x=0.20m, and charge 3 is at x = 0.40m. In addition, the charges have the following values: q1 = -19uC, q2=q3=+19uC. Find the the point where E =0 between x =0.20m?

Find the point where E =0 between x = 0.20m and x = 0.40m

Answer 1

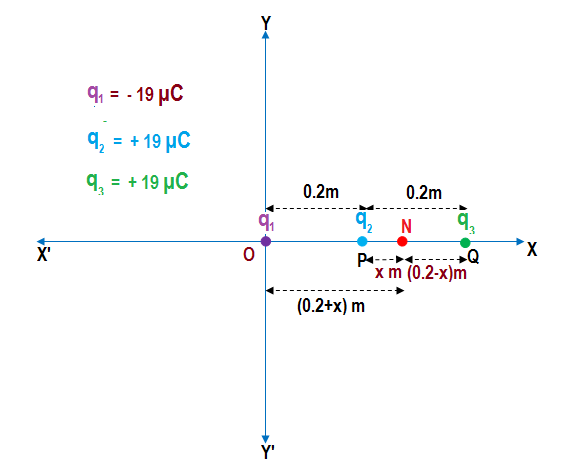
The situation as described in the problem is shown in the figure.
Let the position where the system charges will have net net intensity `E=0` is the point `N` which is `x` m from `q_2`.

Intensity at N due to `q_1`along `vec(NO)=E_1=k_cxx(19xx10^-6)/(0.2+x)^2NC^-1`.

Intensity at N due to `q_3`along `vec(NO)=E_3=k_cxx(19xx10^-6)/(0.2-x)^2NC^-1`.

Intensity at N due to `q_2`along `vec(NQ)=E_2=k_cxx(19xx10^-6)/x^2NC^-1`.

where Coulomb's constant, `k_c=9xx10^9Nm^2"/"C^2`.

So considering the equilibrium we can write

`E_1+E_3=E_2`

`=>k_cxx(19xx10^-6)/(0.2+x)^2+k_cxx(19xx10^-6)/(0.2-x)^2=k_cxx(19xx10^-6)/x^2`

So we have

`1/(0.2+x)^2+1/(0.2-x)^2=1/x^2`

`=>(2xx0.2^2+2xx x^2)/(0.04-x^2)^2=1/x^2`

`=>(0.08+2x^2)/(0.04-x^2)^2=1/x^2`

`=>(0.08+2x^2)x^2=(0.04-x^2)^2`

`=>2x^4+0.08x^2=x^4-0.08x^2+16xx10^-4`

`=>x^4+2xx0.08x^2+(0.08)^2=16xx10^-4+(0.08)^2`

`=>(x^2+0.08)^2=80xx10^-4`

`=>x^2=sqrt(80xx10^-4)-0.08~~0.00944`

`=>x~~sqrt0.00944~~0.09 m`

So location of `N` on x-axis where `E=0` is `color(red)((0.29,0)`