Either of two unit circles passes through the center of the other. How do you prove that the common area is #2/3pi-sqrt 3/2# areal units?

Question

1909 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-09-20T05:11:23

Proved in the explanation

The common area is enclosed by unit circle arcs subtending

#angle120^o=2/3pi# radian, at the respective centers.

For this arc, sector area of a unit circle

#=(2/3pi)/(2pi)#(area of unit circle)=(2/3pi)/(2pi)(pi)=pi/3#

One half of the common area

= this sector area less area of the inner triangle, of sides #[1 ,sqrt 3, 1]#

#=pi/3-(1/2)(sqrt3)(1/2)#

Twice this is the common area =#2/3pi-sqrt 3/2# areal units.

I welcome a graphical depiction,.from an interested reader.

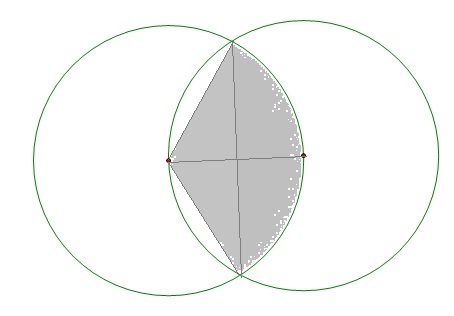
enter image source here

Answer 2 · 2016-09-20T07:10:53

see explanation.

enter image source here

1) Equilateral triangle area #A_e = sqrt((3)/4)xx1^2=sqrt3/4#

2) yellow area #A_y=pi/6-sqrt3/4 = (2pi-3sqrt3)/12#

3) Common area #A_c=2A_e+4A_y#

# A_c=2xxsqrt3/4+4((2pi-3sqrt3)/12)#

#=sqrt3/2+(2pi-3sqrt3)/3#

#=(3sqrt3+4pi-6sqrt3)/6#

#=(4pi-3sqrt3)/6 =2pi/3-sqrt3/2#