How can I calculate the dilution factor using concentration?
1 Answer
Here's how you could do that.
Explanation:
You can start by making sure that you understand what it means to dilute a solution.
The underlying principle when performing a dilution is the fact that the number of moles of solute must remain constant.
As you know, the concentration of a solution is defined as the number of moles of solute per liter of solution.
#color(blue)("molarity" = "moles of solute"/"liter of solution")#
The purpose of a dilution is to decrease the concentration of the solution. Since the number of moles of solute must remain constant, the only way to achieve the decrease in concentration is to increase the volume of the solution by adding more solute.
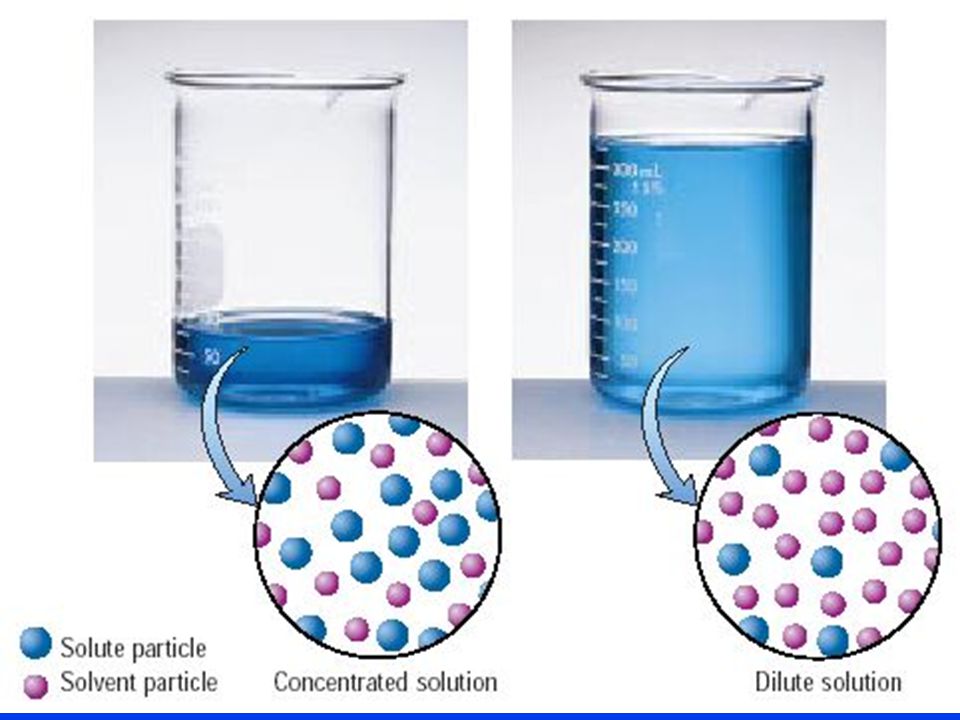
Now, the dilution factor is simply the ratio between the final volume of the diluted solution and the initial volume of the concentrated solution.
#color(blue)("D"."F". = V_"final"/V_"initial")#
Let's say that you don't know the values of the two volumes, which we'll call
#c_1 -># the molarity of the concentrated solution
#c_2 -># the molarity of the diluted solution
Since the number of moles of solute,
#c_1 = n/V_1 " "# and#" "c_2 = n/V_2#
Rearrange to get the volumes of the two solutions
#V_1 = n/c_1" "# and#" "V_2 = n/c_2#
This means that the dilution factor will be
#"D"."F". = V_2/V_1 = V_2 * 1/V_1 = color(red)(cancel(color(black)(n)))/c_2 * c_1/color(red)(cancel(color(black)(n)))#
#"D"."F". = color(green)(c_1/c_2)#
Since the concentration of the stock solution is higher than the concentration of the diluted solution, you can express the former as a multiple of the latter
#c_1 = m xx c_2#
The dilution factor will be
#"D"."F". = (m * color(red)(cancel(color(black)(c_2))))/color(red)(cancel(color(black)(c_2))) = m#
You would thus say that the stock solution was diluted by a factor of
Alternatively, you can say that you performed a

